(本小题满分14分)如图,在五面体 中,四边形
中,四边形 是边长为4的正方形,
是边长为4的正方形, ,平面
,平面
 平面
平面 ,且
,且 ,
, ,点G是EF的中点.
,点G是EF的中点.
(Ⅰ)证明:
 平面
平面 ;
;
(Ⅱ)若直线BF与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求 的长;
的长;
(Ⅲ)判断线段 上是否存在一点
上是否存在一点 ,使
,使 //平面
//平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分10分)已知四棱锥 的底面为直角梯形,
的底面为直角梯形, 底面
底面 ,且
,且 是
是 的中点.
的中点.
(1)证明:平面 平面
平面 ;
;
(2)求 与
与 所成角的余弦值;
所成角的余弦值;
(3)求平面 与平面
与平面 所成二面角(锐角)的余弦值.
所成二面角(锐角)的余弦值.
如图,在多面体 中,四边形
中,四边形 是菱形,
是菱形, 相交于点
相交于点 ,
, ,
, ,平面
,平面
 平面
平面 ,
, ,点
,点 为
为 的中点.
的中点.
(1)求证:直线 平面
平面 ;
;
(2)求证:直线
 平面
平面 .
.
【原创】如图,在正方体 中
中
①求证: 平面
平面 ;
;
②求证: 与平面
与平面 的交点
的交点 是
是 的中心(正三角形五心合一,统称中心)
的中心(正三角形五心合一,统称中心)
在梯形ABCD中,AB∥CD,AB 平面α,CD
平面α,CD 平面α,则直线CD与平面α内的直线的位置关系可能是________.
平面α,则直线CD与平面α内的直线的位置关系可能是________.
【改编】如图,已知 面
面 ,
, ,
, ;
;
(1)在线段 上找一点M,使
上找一点M,使 面
面 。
。
(2)求由面 与面
与面 所成角的二面角的正切值。
所成角的二面角的正切值。
(本小题满分12分)如图,平面 平面
平面 ,其中
,其中 为矩形,
为矩形, 为梯形,
为梯形, ,
, ,
, ,
, 为
为 中点.
中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: .
.
(本小题满分14分)如图,已知 中,
中,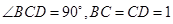 ,
,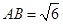 ,
,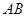 ⊥
⊥
平面 ,
,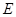 、
、 分别是
分别是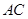 、
、 的中点.
的中点.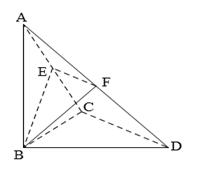
(1)求证:平面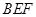 ⊥平面
⊥平面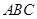 ;
;
(2)设平面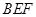
 平面
平面 ,求证
,求证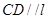 ;
;
(3)求四棱锥B-CDFE的体积V.
(本小题满分12分)如图,在 中,已知
中,已知
 在
在 上,且
上,且 又
又 平面
平面 .
.
(1)求证: ⊥平面
⊥平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
(本小题满分12分)如图,将边长为2的正六边形ABCDEF沿对角线BE翻折,连接AC、FD,形成如图所示的多面体,且

(1)证明:平面ABEF 平面BCDE;
平面BCDE;
(2)求平面ABC与平面DEF所成的二面角(锐角)的余弦值.
如图,在四棱锥P-ABCD中, ,
, ,
, ,
, .
.

(1)求证: 平面
平面 ;
;
(2)若M为线段PA的中点,且过 三点的平面与PB交于点N,求PN:PB的值.
三点的平面与PB交于点N,求PN:PB的值.
已知平面α,β,直线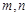 .给出下列命题:
.给出下列命题:
① 若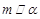 ,
, ,则
,则 ;
;
② 若 ,
, ,则
,则 ;
;
③ 若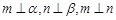 ,则
,则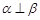 ;
;
④ 若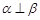 ,
,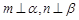 ,则
,则 .
.
其中是真命题的是 .(填写所有真命题的序号).
如图,在四棱锥 中,
中, 平面
平面 ,底面
,底面 是菱形,
是菱形, ,
, ,
, 为
为 与
与 的交点,
的交点, 为棱
为棱 上一点.
上一点.
(Ⅰ)证明:平面 ⊥平面
⊥平面 ;
;
(Ⅱ)若 平面
平面 ,求三棱锥
,求三棱锥 的体积.
的体积.
如图,在三棱柱 中,已知
中,已知 ,
, ,
, ,
, .
.
(1)求证: ;
;
(2)设 (
( ),且平面
),且平面 与
与 所成的锐二面角的大小为30°,试求的值.
所成的锐二面角的大小为30°,试求的值.