高中数学空间向量的应用试题

（本小题满分12分）如图，直三棱柱中，，是棱的中点，．

（Ⅰ）证明：；
（Ⅱ）求二面角的大小．

设是两条不同的直线，是两个不同的平面，则下列命题为真命题个数是    ．
（1）若；
（2）若；
（3）若；
（4）若

如图，在直三棱柱ADE—BCF中，面ABFE和面ABCD都是正方形，M为AB的中点，O为DF的中点．

证明：（1）OM∥平面BCF；
（2）平面MDF⊥平面EFCD．

（本小题满分13分）在如图的几何体中，平面为正方形，平面为等腰梯形，∥，，，．

（Ⅰ）求证：平面；
（Ⅱ）求直线与平面所成角的正弦值．

已知为两条不同的直线，为两个不同的平面，则下列说法正确的是（    ）

A．

B．

C．

D．

设m，n是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是       ．（填写正确命题的序号）
①若m∥n，m⊥β，则 n⊥β；      
②若m∥n，m∥β，则n∥β；
③若m∥α，m∥β，则α∥β；      
④若n⊥α，n⊥β，则α⊥β．

（本小题满分14分）如图，在四棱锥中，平面；四边形是菱形，经过作与平行的平面交与点，的两对角线交点为．
求证：；

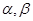设为空间两条不同的直线，为空间两个不同的平面，给出下列命题：
①若，则；      
②若，则；
③若，则；     
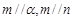④若，则．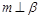
其中的正确命题序号是（  ）

A．③④

B．②④

C．①②

D．①③

如图，四棱锥中，底面为菱形，⊥平面， 交于点是线段中点，为线段中点．

（1）求证：//平面；
（2）求证：⊥．

（本题10分）如图所示，在直三棱柱中，，，、分别为、的中点．

（Ⅰ）求证：；
（Ⅱ）求证：．

已知为两条不同直线，为两个不同平面，给出下列命题:
①       
②
③        
④
其中的正确命题序是（        ）

A．②③

B．③④

C．①②

D．①②③④

已知表示两条不同直线，表示平面，下列说法正确的是（   ）

A．若则

B．若，，则

C．若，，则

D．若，，则

a，b，c表示直线，M表示平面，给出下列四个命题：
①若a∥M，b∥M，则a∥b；
②若bM，a∥b，则a∥M；
③若a⊥c，b⊥c，则a∥b；
④若a⊥M，b⊥M，则a∥b．
⑤a⊥M，bM，若b∥M，则b⊥a
其中正确命题的序号是          ．

如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，，，．

（Ⅰ）求证：平面PQB⊥平面PAD；
（Ⅱ）若二面角M﹣BQ﹣C为30°，设PM=tMC，试确定t的值．

（本小题满分12分）如图，直四棱柱的底面是菱形，侧面是正方形，，是棱的延长线上一点，经过点、、的平面交棱于点，．

（1）求证：平面平面；
（2）求二面角的平面角的余弦值．