设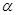 是空间中的一个平面,
是空间中的一个平面,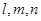 是三条不同的直线,则下列命题中正确的是( )
是三条不同的直线,则下列命题中正确的是( )
A.若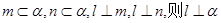 |
B.若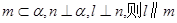 |
C.若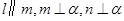 ,则 ,则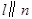 |
D.若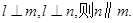 |
(本小题满分12分)如图所示,正方形 和矩形
和矩形 所在平面相互垂直,
所在平面相互垂直, 是
是 的中点.
的中点.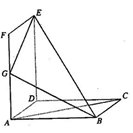
(1)求证: ;
;
(2)若直线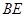 与平面
与平面 成45o角,求异面直线
成45o角,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
(本小题满分12分)如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=PC=2.E是PB的中点.
(1)求证:平面EAC⊥平面PBC;
(2)求二面角P—AC—E的余弦值;
(3)求直线PA与平面EAC所成角的正弦值.
(本小题满分12分)如图所示,正方形 和矩形
和矩形 所在平面相互垂直,
所在平面相互垂直, 是
是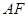 的中点.
的中点.
(1)求证: ;
;
(2)若直线 与平面
与平面 成45o角,求异面直线
成45o角,求异面直线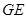 与
与 所成角的余弦值.
所成角的余弦值.
(本小题满分10分)直三棱柱ABC—A′B′C′中,AC=BC=AA′,∠ACB=90°,D、E分别为AB、BB′的中点.
(1)求证:
 ;
;
(2)求证: 平面
平面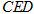 .
.
(本小题满分12分)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.
(Ⅰ)证明:CD⊥平面PAE;
(Ⅱ)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.