类比下列平面内的三个结论所得的空间内的结论成立的是
①平行于同一直线的两条直线平行;
②一条直线如果与两条平行直线中的一条垂直,则必与另一条垂直;
③如果一条直线与两条平行直线中的一条相交,则必与另一条相交.
| A.①②③ | B.①③ | C.① | D.②③ |
已知两条不同的直线 和两个不同的平面
和两个不同的平面 ,有如下命题:
,有如下命题:
①若 ;
;
②若 ;
;
③若 ,其中正确命题的个数是( )
,其中正确命题的个数是( )
| A.3 | B.2 | C.1 | D.0 |
设a,b,c是空间三条直线, ,
, 是空间两个平面,则下列命题中,逆命题不成立的是( )
是空间两个平面,则下列命题中,逆命题不成立的是( )
A.当c⊥ 时,若c⊥ 时,若c⊥ ,则 ,则 ∥ ∥ |
B.当 时,若b⊥ 时,若b⊥ ,则 ,则 |
C.当 ,且c是a在 ,且c是a在 内的射影时,若b⊥c,则a⊥b 内的射影时,若b⊥c,则a⊥b |
D.当 ,且 ,且 时,若c∥ 时,若c∥ ,则b∥c ,则b∥c |
(本小题满分12分)如图,四棱锥 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的 倍,
倍, 为侧棱
为侧棱 上的点.
上的点.
(1)求证: ;
;
(2)若 平面
平面 ,侧棱
,侧棱 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ,若存在,确定点
,若存在,确定点 的位置;若不存在,试说明理由.
的位置;若不存在,试说明理由.
(本小题满分12分)如图,正四棱锥 中,
中, .
.
(1)求证: ;
;
(2)在线段 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的大小为
的大小为 ,若存在,求出
,若存在,求出 ;若不存在,试说明理由.
;若不存在,试说明理由.
如图,在三棱锥 中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,若
中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,若 ,D是PC的中点.
,D是PC的中点.
(1)证明:

 ;
;
(2)求AD与平面ABC所成角的正弦值.
设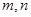 为两条不同的直线,
为两条不同的直线, 为两个不同的平面,下列命题中为真命题的是( )
为两个不同的平面,下列命题中为真命题的是( )
A.若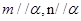 ,则 ,则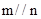 |
B.若 ,则 ,则 |
C.若 ,则 ,则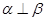 |
D.若 ,则 ,则 |
如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )

①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行
| A.0 | B.1 | C.2 | D.3 |
如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.
(Ⅰ)试证:AB⊥平面BEF;
(Ⅱ)设PA=k•AB,且二面角E﹣BD﹣C的平面角大于45°,求k的取值范围.
如图,在四棱锥S﹣ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC上一点.
(Ⅰ)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(Ⅱ)求证:平面BDE⊥平面SAC;
(Ⅲ)(理科)当二面角E﹣BD﹣C的大小为45°时,试判断点E在SC上的位置,并说明理由.
(本小题12分)
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=BC,D、E、F分别为棱AB、BC、A1C1的中点。
(Ⅰ)证明:EF//平面A1CD;
(Ⅱ)证明:平面A1CD⊥平面ABB1A1。
(本小题满分14分)如图,平面PAC⊥平面ABC,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO的中点,AB=BC=AC=4,PA=PC=2 .求证:
.求证:
(1)PA⊥平面EBO;
(2)FG∥平面EBO.