高中数学立体图形的结构特征试题

在半径为5的球面上有不同的四点A、B、C、D，若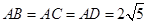，则平面BCD被球所截面图形的面积为.

如图，在空间四边形中，两条对角线互相垂直，且长度分别为4和6，平行于这两条对角线的平面与边分别相交于点，记四边形的面积为y，设，则（）

A．函数的值域为

B．函数的最大值为8

C．函数在上单调递减

D．函数满足

如图，点,, ,分别是四面体的顶点或其棱的中点，则在同一平面内的四点组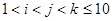（）共有个.

如图，圆锥的轴截面SAB是边长为2的等边三角形，O为底面中心，M为SO中点，动点P在圆锥底面内（包括圆周），若AM⊥MP，则点P形成的轨迹长度为

如图所示，设计一个四棱锥形冷水塔塔顶，四棱锥的底面是正方形，侧面是全等的等腰三角形，已知底面边长为2m，高为m，制造这个塔顶需要多少铁板？

已知直三棱柱ABC-A₁B₁C₁的各棱长均为1,棱BB₁所在直线上的动点M满足,AM与侧面BB₁C₁C所成的角为,若,则的取值范围是（）

A．

B．

C．

D．

长方体的一个顶点上三条棱长分别是3，4，5，且它的8个顶点都在同一球面上，则这个球的表面积是．

如图，在长方形ABCD中，AB=，BC=1，E为线段DC上一动点，现将AED沿AE折起，使点D在面ABC上的射影K在直线AE上，当E从D运动到C，则K所形成轨迹的长度为．

如图，在长方形ABCD中，AB=，BC=1，E为线段DC上一动点，现将AED沿AE折起，使点D在面ABC上的射影K在直线AE上，当E从D运动到C，则K所形成轨迹的长度为（）

A．

B．

C．

D．

如图，取一个底面半径和高都为R的圆柱，从圆柱中挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥，把所得的几何体与一个半径为R的半球放在同一水平面上．用一平行于平面的平面去截这两个几何体，截面分别为圆面和圆环面（图中阴影部分）．设截面面积分别为和，那么

A．

B．=

C．

D．不确定

如图，正方体的棱长为，点在棱上，且，点是平面上的动点，且动点到直线的距离与点到点的距离的平方差为，则动点的轨迹是（）

A．圆

B．抛物线

C．双曲线

D．椭圆

已知一圆柱内接于球，且圆柱的底面直径与母线长均为，则球的表面积为．

抛物线绕轴旋转一周形成一个如图所示的旋转体，在此旋转体内水平放入一个正方体，使正方体的一个面恰好与旋转体的开口面平齐，则此正方体的棱长是．

如图直三棱柱ABB₁-DCC₁中， BB₁⊥AB，AB=4，BC=2，CC₁=1，DC上有一动点P，则△APC₁周长的最小值是.

一个棱长为6的正四面体纸盒内放一个正方体，若正方体可以在纸盒内任意转动，则正方体棱长的最大值为