下列命题正确的有
①用相关指数 来刻画回归效果,
来刻画回归效果, 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好;
②命题 :“
:“ ”的否定
”的否定 :“
:“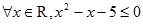 ”;
”;
③设随机变量 服从正态分布
服从正态分布 , 若
, 若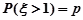 ,则
,则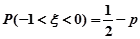 ;
;
④回归直线一定过样本中心(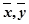 ).
).
| A.1个 | B.2个 | C.3个 | D.4个 |
(本小题12分)下表提供了工厂技术改造后某种型号设备的使用年限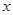 和所支出的维修费用
和所支出的维修费用 (万元)的几组对照数据:
(万元)的几组对照数据:
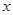 (年) (年) |
 |
 |
 |
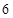 |
 (万元) (万元) |
 |
 |
 |
 |
(1)若知道 对
对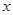 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出 关于
关于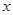 的线性回归方程
的线性回归方程 ;
;
(2)已知工厂技改前该型号设备使用10年的维修费用为9万元.试根据(1)求出的线性回归方程,预测该型号设备技改后使用10年的维修费用比技改前降低多少?
某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1) 求出y关于x的线性回归方程;
(2) 试预测加工10个零件需要多少时间?
(本小题满分13分)某同学大学毕业后在一家公司上班,工作年限 和年收入
和年收入 (万元),有以下的统计数据:
(万元),有以下的统计数据:
 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(Ⅲ)请你估计该同学第8年的年收入约是多少?
(参考公式: )
)
(本小题10分)某种产品的广告费用支出 与销售额
与销售额 之间有如下的对应数据:
之间有如下的对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
50 |
60 |
70 |
(1)求 对
对 的回归直线方程;
的回归直线方程;
(2)据此估计广告费用为10销售收入 的值.
的值.
参考公式:
某企业的某种产品产量与单位成本统计数据如下:
| 月份 |
1 |
2 |
3 |
4 |
5 |
6 |
| 产量(千件) |
2 |
3 |
4 |
3 |
4 |
5 |
| 单位成本(元/件) |
73 |
72 |
71 |
73 |
69 |
68 |

(用最小二乘法求线性回归方程系数公式
注: ,
, )
)
(1)试确定回归方程;
(2)指出产量每增加1 件时,单位成本下降多少?
(3)假定产量为6 件时,单位成本是多少?单位成本为70元/件时,产量应为多少件?
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据。
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(2)已知该厂技改前 吨甲产品的生产能耗为
吨甲产品的生产能耗为 吨标准煤.试根据(2)求出的线性回归方程,预测生产
吨标准煤.试根据(2)求出的线性回归方程,预测生产 吨甲产品的生产能耗比技改前降低多少吨标准煤?
吨甲产品的生产能耗比技改前降低多少吨标准煤?
(线性回归方程 中的系数
中的系数 可以用公式
可以用公式 )
)
某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人,不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人.
(1)根据以上数据建立一个 的列联表;
的列联表;
(2)认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?(参考数值: )
)
一次兴趣调查,共调查了1000名学生,其中男女生各500名,喜欢数学的男260名,喜欢数学的女生有220名.
(1)根据以上数据作出2×2列联表
(2)运用独立性检验思想,判断喜欢数学与性别是否有关系?(要求达到99.9%才能认定为有关系)
参考数据与公式:
临界值表
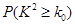 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
某种产品的广告费支出 与销售额
与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
(Ⅰ)求回归直线方程;(参考公式:b= ,
, )
)
(Ⅱ)试预测广告费支出为10万元时,销售额多大?
(参考数据:

 )
)
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验如下:
零件的个数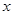 (个) (个) |
2 |
3 |
4 |
5 |
加工的时间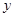 (小时) (小时) |
2.5 |
3 |
4 |
4.5 |
(1)在给定坐标系中画出表中数据的散点图;
(2)求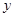 关于
关于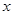 的线性回归方程
的线性回归方程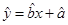 ;
;
(3)试预测加工10个零件需要多少时间?
(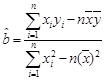 ,
,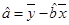 )
)
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程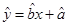 ;
;
(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
(相关公式: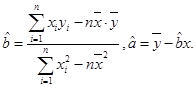 )
)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量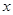 (吨)与相应的生产能耗
(吨)与相应的生产能耗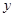 (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
 |
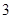 |
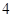 |
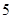 |
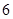 |
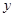 |
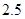 |
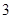 |
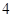 |
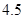 |
(1)请根据上表提供的数据,求出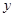 关于
关于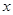 的线性回归方程
的线性回归方程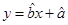 ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?