(本小题满分12分)在等差数列 中,
中,
(Ⅰ)求通项 ;
;
(Ⅱ)求此数列前30项的绝对值的和.
(本小题满分12分)已知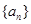 为等差数列,且满足
为等差数列,且满足 ,
,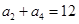 .
.
(Ⅰ)求数列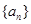 的通项公式;
的通项公式;
(Ⅱ)记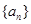 的前
的前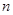 项和为
项和为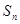 ,若
,若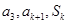 成等比数列,求正整数
成等比数列,求正整数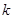 的值.
的值.
(本小题满分14分)已知等差数列 的公差
的公差 ,它的前
,它的前 项和为
项和为 ,若
,若 ,且
,且 ,
, ,
, 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
已知等差数列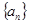 的公差为
的公差为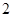 ,且
,且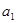 ,
,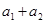 ,
,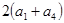 成等比数列.
成等比数列.
(Ⅰ)求数列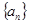 的通项公式;
的通项公式;
(Ⅱ)设数列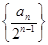 的前
的前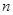 学科王项和为
学科王项和为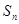 ,求证:
,求证: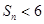 .
.
设公差不为0的等差数列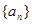 的首项为1,且
的首项为1,且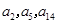 构成等比数列.
构成等比数列.
(Ⅰ)求数列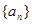 的通项公式;
的通项公式;
(Ⅱ)若数列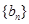 满足
满足 …
…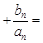 1-
1-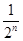 ,n∈N*,求
,n∈N*,求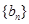 的前n项和
的前n项和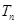 .
.
已知数列满足:,数列满足:,,数列的前项和为.
(1)求证:数列为等比数列;
(2)求证:数列为递增数列;
(3)若当且仅当时,取得最小值,求的取值范围.
已知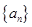 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,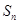 为
为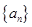 的前
的前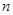 项和.
项和.
(1)求通项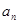 及
及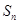 ;
;
(2)设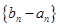 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列 的通项公式及其前
的通项公式及其前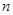 项和
项和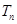 .
.
等差数列 的前n项和为
的前n项和为 ,已知
,已知 ,
, 为整数,且
为整数,且 .
.
(1)求 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前n项和
的前n项和 .
.
已知等比数列 满足:
满足: 公比
公比 ,数列
,数列 的前
的前 项和为
项和为 ,且
,且 (
( ).
).
(1)求数列 和数列
和数列 的通项
的通项 和
和 ;
;
(2)设 ,证明:
,证明:
已知 是等比数列
是等比数列 的前n项的和,
的前n项的和, 成等差数列.
成等差数列.
(1)求等比数列 的公比
的公比 ;
;
(2)判断 是否成等差数列?若成等差数列,请给出证明;若不成等差数列,说明理由
是否成等差数列?若成等差数列,请给出证明;若不成等差数列,说明理由
已知等差数列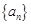 满足:
满足: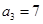 ,
,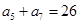 .
.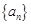 的前n项和为
的前n项和为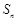 .
.
(Ⅰ)求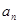 及
及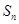 ;
;
(Ⅱ)令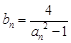 (
( ),求数列
),求数列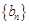 的前n项和
的前n项和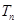 .
.