如图,在三棱锥 中,平面
中,平面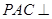 平面
平面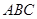 ,
,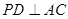 于点
于点 ,且
,且 ,
, ,
,
(1)求证:
(2)
(3)若 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
如图,直四棱柱中,
,
,
,
,
,
为
上一点,
,

(1)证明:平面
;
(2)求点到平面
的距离。
如图,点(0,﹣1)是椭圆
:
的一个顶点,
的长轴是圆
:
的直径,
,
是过点
且互相垂直的两条直线,其中
交圆
于
两点,
交椭圆
于另一点
.
(1)求椭圆的方程;
(2)求面积的最大值时直线
的方程.

已知函数
.
(1)求函数
的单调区间;
(2)证明:对任意的
,存在唯一的
,使
.
(3)设(2)中所确定的
关于
的函数为
,证明:当
时,有
.
已知首项为
的等比数列
不是递减数列,其前
项和为
,且
成等差数列.
(1)求数列
的通项公式;
(2)设
,求数列
的最大项的值与最小项的值.
已知函数,
为常数且
.
(1)证明:函数的图像关于直线
对称;
(2)若满足
,但
,则
称为函数
的二阶周期点,如果
有两个二阶周期点
,试确定
的取值范围;
(3)对于(2)中的,和
,设
为函数
的最大值点,
,记
的面积为
,讨论
的单调性.
如图,已知椭圆与
的中心在坐标原点
,长轴均为
且在
轴上,短轴长分别为
,过原点且不与
轴重合的直线l
与
的四个交点按纵坐标从大到小依次为
,记
,
和
的面积分别为
和
.
(1)当直线轴重合时,若
,求
的值;
(2)当变化时,是否存在与坐标轴不重合的直线
,使得
?并说明理由.

设函数定义在
上,
,导函数
,
.
(1)求的单调区间和最小值;
(2)讨论与
的大小关系;
(3)是否存在,使得
对任意
成立?若存在,求出
的取值范围;若不存在,请说明理由.
已知函数 (
( ) =
) = ,g (
,g ( )=
)= +
+ 。
。
(1)求函数h ( )=
)= (
( )-g (
)-g ( )的零点个数,并说明理由;
)的零点个数,并说明理由;
(2)设数列 满足
满足 ,
, ,证明:存在常数
,证明:存在常数,使得对于任意的
 ,都有
,都有 ≤
≤  .
.
如图,椭圆的离心率为
,
轴被曲线
截得的线段长等于
的长半轴长。

(1)求,
的方程;
(2)设与
轴的交点为
,过坐标原点
的直线
与
相交于点
,直线
分别与
相交与
.
①证明:;
②记的面积分别是
.问:是否存在直线
,使得
=
 ?请说明理由。
?请说明理由。
设直线与函数
的图像分别交于点
,则当
达到最小时
的值为()
| A. | 1 | B. |
|
C. |
|
D. |
|
设椭圆C1: =1(a>b>0)的左、右焦点分别为为
=1(a>b>0)的左、右焦点分别为为 ,
, 恰是抛物线C2:
恰是抛物线C2: 的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
的焦点,点M为C1与C2在第一象限的交点,且|MF2|= .
.
(1)求C1的方程;
(2)平面上的点N满足 ,直线l∥MN,且与C1交于A,B两点,若
,直线l∥MN,且与C1交于A,B两点,若 ,求直线l的方程.
,求直线l的方程.
如果函数 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”。
性质”。
(1)判断函数 是否具有“
是否具有“ 性质”,若具有“
性质”,若具有“ 性质”,求出所有
性质”,求出所有 的值;若不具有“
的值;若不具有“ 性质”,说明理由;
性质”,说明理由;
(2)已知 具有“
具有“ 性质”,且当
性质”,且当 时
时 ,求
,求 在
在 上有最大值;
上有最大值;
(3)设函数 具有“
具有“ 性质”,且当
性质”,且当 时,
时, .若
.若 与
与 交点个数为2013,求
交点个数为2013,求 的值.
的值.
已知在 的展开式中,第5项的系数与第3项的系数之比是
的展开式中,第5项的系数与第3项的系数之比是 .
.
(1)求展开式中的所有有理项;
(2)求展开式中系数绝对值最大的项;
(3)求 的值.
的值.
设 和
和 是函数
是函数 的两个极值点,其中
的两个极值点,其中 .
.
(1)求 的取值范围;
的取值范围;
(2)若 为自然对数的底数),求
为自然对数的底数),求 的最大值.
的最大值.