如果函数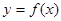 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意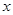 ,存在实数
,存在实数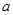 使得
使得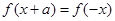 成立,则称此函数具有“
成立,则称此函数具有“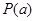 性质”。
性质”。
(1)判断函数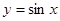 是否具有“
是否具有“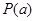 性质”,若具有“
性质”,若具有“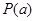 性质”,求出所有
性质”,求出所有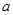 的值;若不具有“
的值;若不具有“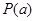 性质”,说明理由;
性质”,说明理由;
(2)已知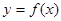 具有“
具有“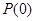 性质”,且当
性质”,且当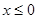 时
时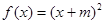 ,求
,求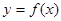 在
在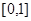 上有最大值;
上有最大值;
(3)设函数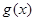 具有“
具有“ 性质”,且当
性质”,且当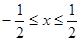 时,
时,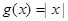 .若
.若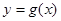 与
与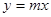 交点个数为2013,求
交点个数为2013,求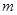 的值.
的值.
相关知识点
推荐套卷
如果函数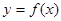 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意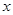 ,存在实数
,存在实数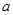 使得
使得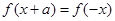 成立,则称此函数具有“
成立,则称此函数具有“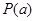 性质”。
性质”。
(1)判断函数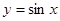 是否具有“
是否具有“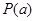 性质”,若具有“
性质”,若具有“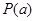 性质”,求出所有
性质”,求出所有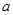 的值;若不具有“
的值;若不具有“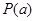 性质”,说明理由;
性质”,说明理由;
(2)已知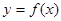 具有“
具有“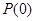 性质”,且当
性质”,且当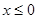 时
时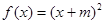 ,求
,求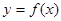 在
在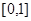 上有最大值;
上有最大值;
(3)设函数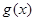 具有“
具有“ 性质”,且当
性质”,且当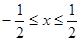 时,
时,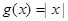 .若
.若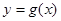 与
与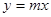 交点个数为2013,求
交点个数为2013,求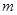 的值.
的值.