某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 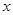 (个) (个) |
2 |
3 |
4 |
5 |
加工的时间  (小时) (小时) |
2.5 |
3 |
4 |
4.5 |
(1)求出 关于
关于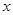 的线性回归方程
的线性回归方程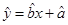 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;

(2)试预测加工 个零件需要多少小时?
个零件需要多少小时?
(注: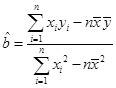 ,
, ,
, ,
,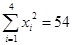 )
)
如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( )

| A.2,5 | B.5,5 | C.5,8 | D.8,8 |
设函数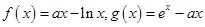 ,其中
,其中 为正实数.
为正实数.
(Ⅰ)若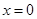 是函数
是函数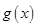 的极值点,讨论函数
的极值点,讨论函数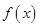 的单调性;
的单调性;
(Ⅱ)若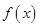 在
在 上无最小值,且
上无最小值,且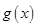 在
在 上是单调增函数,求
上是单调增函数,求 的取值范围,并由此判断曲线
的取值范围,并由此判断曲线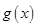 与曲线
与曲线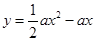 在
在 交点个数.
交点个数.
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为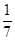 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.用
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.用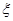 表示取球终止时所需要的取球次数.
表示取球终止时所需要的取球次数.
(1)求袋中原有白球的个数;
(2)求随机变量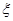 的概率分布;
的概率分布;
(3)求甲取到白球的概率.
已知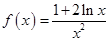 .
.
(1)求 的单调区间;
的单调区间;
(2)令 ,则
,则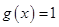 时有两个不同的根,求
时有两个不同的根,求 的取值范围;
的取值范围;
(3)存在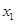 ,
,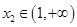 且
且 ,使
,使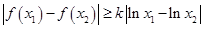 成立,求
成立,求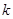 的取值范围.
的取值范围.
已知函数 的导数
的导数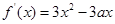 ,
,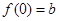 ,(a,b为实数),
,(a,b为实数),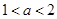 .
.
(1)若 在区间
在区间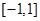 上的最小值、最大值分别为
上的最小值、最大值分别为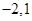 ,求a,b的值;
,求a,b的值;
(2)设函数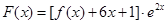 ,试判断函数
,试判断函数 的极值点个数.
的极值点个数.
正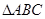 的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将
的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将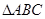 沿CD翻折成直二面角A-DC-B.
沿CD翻折成直二面角A-DC-B.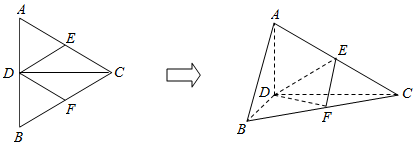
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角E-DF-C的余弦值;
(3)在线段BC上是否存在一点P,使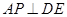 ?若存在,请指出P点的位置,若存在,请说明理由.
?若存在,请指出P点的位置,若存在,请说明理由.
已知抛物线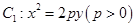 与圆
与圆 的两个交点之间的距离为4.
的两个交点之间的距离为4.
(1)求 的值;
的值;
(2)设过抛物线 的焦点
的焦点 且斜率为
且斜率为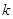 的直线与抛物线交于
的直线与抛物线交于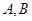 两点,与圆
两点,与圆 交于
交于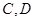 两点,当
两点,当 时,求
时,求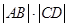 的取值范围.
的取值范围.