在△ABC中,角A,B,C对应的边分别是a,b,c,已知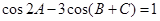 .
.
(1)求角A的大小;
(2)若△ABC的面积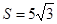 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
已知点P,A,B,C,D是球O表面上的点,PA⊥平面ABCD,四边形ABCD是边长为 的正方形.若
的正方形.若 ,则△OAB的面积为_______.
,则△OAB的面积为_______.
已知某几何体的三视图和直观图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.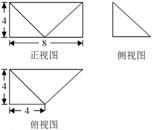

(Ⅰ)求证: ;
;
(Ⅱ)求直线 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(Ⅲ)设 为
为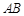 中点,在棱
中点,在棱 上是否存在一点
上是否存在一点 ,使
,使 平面
平面 ?若存在,求
?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为 .
.
如图,在三棱锥 中,平面
中,平面 平面
平面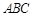 ,
, 为等边三角形,
为等边三角形, ,且
,且 ,O,M分别为
,O,M分别为 ,
, 的中点.
的中点.
(Ⅰ)求证: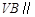 平面
平面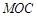 ;
;
(Ⅱ)设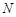 是线段
是线段 上一点,满足平面
上一点,满足平面 平面
平面 ,试说明点的位置
,试说明点的位置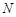 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
如图,正方体 的棱长为1,P为BC的中点,Q为线段
的棱长为1,P为BC的中点,Q为线段 上的动点,过
上的动点,过
点A,P,Q的平面截该正方体所得的截面记为S.给出下列命题:

①当 时,S为四边形;
时,S为四边形;
②当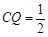 时,S为等腰梯形;
时,S为等腰梯形;
③当 时,S与C1D1的交点R满足
时,S与C1D1的交点R满足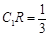 ;
;
④当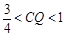 时,S为六边形;
时,S为六边形;
⑤当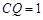 时,S的面积为
时,S的面积为 其中正确的是( )
其中正确的是( )
| A.①②③ | B.①②③⑤ | C.②③④⑤ | D.①③④⑤ |
下列说法中,不正确的是( )
A.已知 ,命题“若 ,命题“若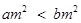 ,则 ,则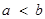 ”为真命题; ”为真命题; |
B.命题“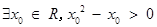 ”的否定是:“ ”的否定是:“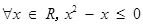 ”; ”; |
C.命题“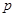 或 或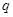 ”为真命题,则命题 ”为真命题,则命题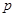 和命题 和命题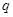 均为真命题; 均为真命题; |
D.“ ”是“ ”是“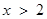 ”的充分不必要条件. ”的充分不必要条件. |