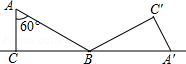
如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A′处,若AO=OB=1,则阴影部分面积为( )

A. πB. π﹣1C. +1D.
如图,在Rt△ ABC中,∠ C=90°, AC=3, BC=4,把△ ABC绕 AB边上的点 D顺时针旋转90°得到△ A′ B′ C′, A′ C′交 AB于点 E,若 AD= BE,则△ A′ DE的面积是 .

如图,在Rt△ ABC中,∠ C=90°, M为 AB边的中点,将Rt△ ABC绕点 M旋转,使点 C与点 A重合得△ DEA, AE交 CB于点 N.若 AB=2 , AC=4,则 CN的长为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在Rt△ ABC中,∠ B=90°, AB= BC=2,将△ ABC绕点 C顺时针旋转60°,得到△ DEC,则 AE的长是 .

如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点A旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )

A.πcmB.2πcmC.3πcmD.5πcm
如图,网格纸上正方形小格的边长为1.图中线段 和点
和点 绕着同一个点做相同的旋转,分别得到线段
绕着同一个点做相同的旋转,分别得到线段 和点
和点 ,则点
,则点 所在的单位正方形区域是
所在的单位正方形区域是


A.1区B.2区C.3区D.4区
如图, 和
和 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形, ,点
,点 为射线
为射线 ,
, 的交点.
的交点.
(1)求证: ;
;
(2)若 ,
, ,把
,把 绕点
绕点 旋转,
旋转,
①当 时,求
时,求 的长;
的长;
②直接写出旋转过程中线段 长的最小值与最大值.
长的最小值与最大值.

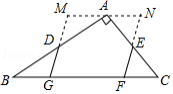
如图,在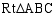 中,
中,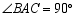 ,
,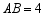 ,
,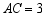 ,点
,点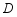 、
、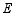 分别是
分别是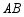 、
、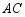 的中点,点
的中点,点 、
、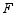 在
在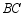 边上(均不与端点重合),
边上(均不与端点重合),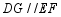 .将
.将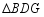 绕点
绕点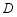 顺时针旋转
顺时针旋转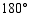 ,将
,将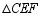 绕点
绕点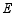 逆时针旋转
逆时针旋转 ,拼成四边形
,拼成四边形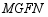 ,则四边形
,则四边形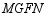 周长
周长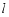 的取值范围是 .
的取值范围是 .
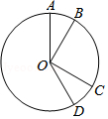
如图, 的半径为3,点
的半径为3,点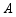 ,
,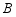 ,
,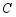 ,
,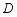 在
在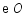 上,
上,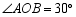 ,将扇形
,将扇形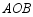 绕点
绕点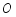 顺时针旋转
顺时针旋转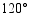 后恰好与扇形
后恰好与扇形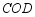 重合,则
重合,则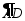 的长为
的长为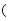
A.
B.
C.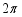 D.
D.
如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.
(1)求证:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF,求BE.

如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是 .

如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )

A.πB. C.3+πD.8﹣π
如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.

如图,△ABC中,∠C=90°,∠A=60°, .将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是 .