如图,长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°,则点A翻滚到A2位置时共走过的路径长为( )

| A.10cm | B. cm cm |
C. cm cm |
D. cm cm |
如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则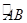 的长为( )
的长为( )

| A.π | B.6π | C.3π | D.1.5π |
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:

①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③∠AOB=150°;
④四边形AO BO′的面积为 ;
;
⑤ .
.
其中正确的结论是( )
| A.①②③ | B.①②③④ | C.①②③⑤ | D.①②③④⑤ |
用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为______度.
(年新疆、生产建设兵团)如图,在矩形ABCD中,CD=1,∠DBC=30°.若将BD绕点B旋转后,点D落在DC延长线上的点E处,点D经过的路径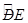 ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )

A.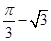 |
B. |
C.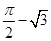 |
D.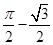 |
(年贵州省遵义市)将正方形ABCD绕点A按逆时针方向旋转 ,得正方形
,得正方形 ,
, 交CD于点E,AB=
交CD于点E,AB= ,则四边形
,则四边形 的内切圆半径为( ).
的内切圆半径为( ).

A. |
B. |
C. |
D. |
(年青海省中考)一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )

| A.105° | B.115° | C.120° | D.135° |
(年贵州省黔南州)如图,在平面直角坐标系xOy中,抛物线 过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB,过点B作x轴的垂线,过点A作y轴的垂线,两直线交于点D.
过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB,过点B作x轴的垂线,过点A作y轴的垂线,两直线交于点D.
(1)求b、c的值;
(2)当t为何值时,点D落在抛物线上;
(3)是否存在t,使得以A,B,D为顶点的三角形与△AOP相似?若存在,求此时t的值;若不存在,请说明理由.
如图,将含30°角的直角三角尺ABC绕点B顺时针旋转 
150°后得到△EBD,连结CD.若AB="4cm." 则△BCD的面积
为( )
A.4 B.2 C.3 D.2
(本题12分)已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G,∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.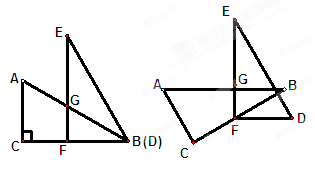
(1)求证:△EGB是等腰三角形
(2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小 度时,四边形ACDE成为以ED为底的梯形(如图(2)),求此梯形的高。
如图, 绕点
绕点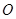 逆时针旋转
逆时针旋转 到
到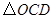 的位置,已知
的位置,已知 ,则
,则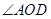 等于( ).
等于( ).
A.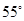 |
B.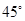 |
C.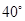 |
D.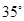  |