如图, 是 的内接三角形,点 在 上,点 在弦 上 不与 重合),且四边形 为菱形.
(1)求证: ;
(2)求证: ;
(3)已知 的半径为3.
①若 ,求 的长;
②当 为何值时, 的值最大?

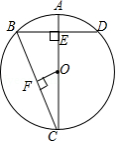
如图,公园内有一个半径为20米的圆形草坪, , 是圆上的点, 为圆心, ,从 到 只有路 ,一部分市民为走“捷径”,踩坏了花草,走出了一条小路 .通过计算可知,这些市民其实仅仅少走了 步(假设1步为0.5米,结果保留整数).(参考数据: , 取

如图,已知 为 直径, 是 的切线,连接 交 于点 ,取 的中点 ,连接 交 于点 ,过点 作 于 .
(1)求证: ;
(2)若 , ,求 和 的长.
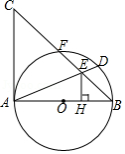
如图, 是 的直径,弦 于 ,连接 ,过点 作 于 ,若 , ,则 的长度是
A. B. C. D.
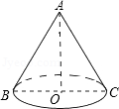
如图, 是圆锥的母线, 为底面直径,已知 ,圆锥的侧面积为 ,则 的值为
A. B. C. D.
如图1,直线 与 轴交于点 ,与 轴交于点 ,点 是线段 上一动点 .以点 为圆心, 长为半径作 交 轴于另一点 ,交线段 于点 ,连接 并延长交 于点 .

(1)求直线 的函数表达式和 的值;
(2)如图2,连接 ,当 时,
①求证: ;
②求点 的坐标;
(3)当点 在线段 上运动时,求 的最大值.
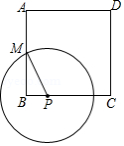
如图,正方形 的边长为8, 是 的中点, 是 边上的动点,连接 ,以点 为圆心, 长为半径作 .当 与正方形 的边相切时, 的长为 .
如图,在 中, , , ,以点 为圆心, 长为半径画弧,交边 于点 ,则 的长为

A. B. C. D.
如图,在 中,点 在斜边 上,以 为圆心, 为半径作圆,分别与 , 相交于点 , ,连接 .已知 .
(1)求证: 是 的切线.
(2)若 , ,求 的半径.

如图1是小明制作的一副弓箭,点 , 分别是弓臂 与弓弦 的中点,弓弦 .沿 方向拉动弓弦的过程中,假设弓臂 始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点 拉到点 时,有 , .
(1)图2中,弓臂两端 , 的距离为 .
(2)如图3,将弓箭继续拉到点 ,使弓臂 为半圆,则 的长为 .
