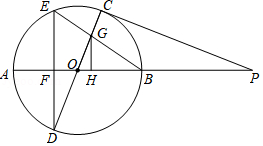
如图,已知 , 是 的直径,过点 作 的切线交 的延长线于点 , 的弦 交 于点 ,且 .
(1)求证: ;
(2)连接 交 于点 ,过点 作 于点 ,若 , ,求 的长.
如图,在 中, , , ,以点 为原点建立平面直角坐标系,使 在 轴正半轴上,点 是 边上的一个动点, 交 于 , 于 , 于 .以下结论:
① ;
②当 为 的中点时, ;
③点 的坐标为 ;
④将 沿 所在的直线翻折到原来的平面,点 的对应点 的坐标为 ;
⑤矩形 的最大面积为3.在这些结论中正确的有 (只填序号)

如图1,在四边形 中, , , ,垂足分别为 , , , ,点 , , 分别为 , , 的中点,连接 , , .

(1)如图2,当 , , 时,求 的值;
(2)若 , ,则可求出图中哪些线段的长?写出解答过程;
(3)连接 , , , .试证明 与 全等;
(4)在(3)的条件下,图中还有哪些其它的全等三角形?请直接写出.
正方形 的边长为1,点 是 边上的一个动点(与 , 不重合),以 为顶点在 所在直线的上方作 .
(1)当 经过点 时,
①请直接填空: (可能,不可能)过 点;(图1仅供分析)
②如图2,在 上截取 ,过 点作 垂直于直线 ,垂足为点 ,作 于 ,求证:四边形 为正方形.
(2)当 不过点 时,设 交边 于 ,且 .在 上存在点 ,过 点作 垂直于直线 ,垂足为点 ,使得 ,连接 ,求四边形 的最大面积.

如图,在四边形 中, , , , , ,将 绕点 顺时针方向旋转后得△ ,当 恰好经过点 时,△ 为等腰三角形,则
A. B. C. D.
如图,在四边形 中, , , 的平分线 交 于点 , ,点 恰好为 的中点,若 , ,则

A.1B.2C.3D.4
在四边形 中, , , , .以 为腰作等腰 ,使 ,过点 作 交直线 于点 .请画出图形,并直接写出 的长.
如图,方格纸中每个小正方形的边长均为1,线段 的两个端点均在小正方形的顶点上.
(1)在图中画出以线段 为一边的矩形 (不是正方形),且点 和点 均在小正方形的顶点上;
(2)在图中画出以线段 为一腰,底边长为 的等腰三角形 ,点 在小正方形的顶点上,连接 ,请直接写出线段 的长.

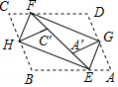
如图,平行四边形纸片 的边 , 的长分别是 和 ,将其四个角向内对折后,点 与点 重合于点 ,点 与点 重合于点 .四条折痕围成一个“信封四边形” ,其顶点分别在平行四边形 的四条边上,则 .
如图,在 中, ,且 , ,点 是斜边 上的一个动点,过点 分别作 于点 , 于点 ,连接 ,则线段 的最小值为 .

如图1,已知 是 的外接圆, 的平分线 交 于点 ,交 于点 ,连接 , .
(1)求证: ;
(2)如图2,在图1的基础上做 的直径 交 于点 ,连接 ,过点 做 的切线 ,若 ,求 的度数;
(3)在(2)的条件下,若 的面积为 , 与 的面积比为 ,求 的长.

已知: 、 两点在直线 的同一侧,线段 , 均是直线 的垂线段,且 在 的右边, ,将 沿直线 向右平移,在平移过程中,始终保持 不变, 边与直线 相交于点 .
(1)当 与 重合时(如图2所示),设点 是 的中点,连接 .求证:四边形 是正方形;
(2)请利用如图1所示的情形,求证: ;
(3)若 ,且当 时,请直接写出 和 的长.

如图,矩形 的四个顶点分别在矩形 的各条边上, , , .有以下四个结论:① ;② ;③ ;④矩形 的面积是 .其中一定成立的是 .(把所有正确结论的序号填在横线上)

问题情境:
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将:矩形纸片 沿对角线 剪开,得到 和 .并且量得 , .
操作发现:
(1)将图1中的 以点 为旋转中心,按逆时针方向旋转 ,使 ,得到如图2所示的△ ,过点 作 的平行线,与 的延长线交于点 ,则四边形 的形状是 .
(2)创新小组将图1中的 以点 为旋转中心,按逆时针方向旋转,使 、 、 三点在同一条直线上,得到如图3所示的△ ,连接 ,取 的中点 ,连接 并延长至点 ,使 ,连接 、 ,得到四边形 ,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将 沿着 方向平移,使点 与点 重合,此时 点平移至 点, 与 相交于点 ,如图4所示,连接 ,试求 的值.

再读教材:
宽与长的比是 (约为 的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,下面,我们用宽为2的矩形纸片折叠黄金矩形.(提示:
第一步,在矩形纸片一端,利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②,把这个正方形折成两个相等的矩形,再把纸片展平.

第三步,折出内侧矩形的对角线 ,并把 折到图③中所示的 处.
第四步,展平纸片,按照所得的点 折出 ,使 ,则图④中就会出现黄金矩形.

问题解决:
(1)图③中 (保留根号);
(2)如图③,判断四边形 的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
实际操作
(4)结合图④,请在矩形 中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.