正方形 的边长为1,点 是 边上的一个动点(与 , 不重合),以 为顶点在 所在直线的上方作 .
(1)当 经过点 时,
①请直接填空: (可能,不可能)过 点;(图1仅供分析)
②如图2,在 上截取 ,过 点作 垂直于直线 ,垂足为点 ,作 于 ,求证:四边形 为正方形.
(2)当 不过点 时,设 交边 于 ,且 .在 上存在点 ,过 点作 垂直于直线 ,垂足为点 ,使得 ,连接 ,求四边形 的最大面积.
推荐套卷
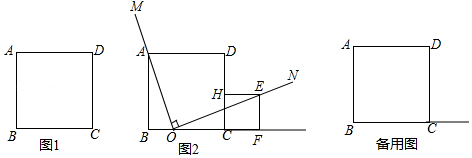
正方形 的边长为1,点 是 边上的一个动点(与 , 不重合),以 为顶点在 所在直线的上方作 .
(1)当 经过点 时,
①请直接填空: (可能,不可能)过 点;(图1仅供分析)
②如图2,在 上截取 ,过 点作 垂直于直线 ,垂足为点 ,作 于 ,求证:四边形 为正方形.
(2)当 不过点 时,设 交边 于 ,且 .在 上存在点 ,过 点作 垂直于直线 ,垂足为点 ,使得 ,连接 ,求四边形 的最大面积.
