初中数学一元二次方程试题

某网络经销商销售一款夏季时装，进价每件60元，售价每件130元，每天销售30件，每销售一件需缴纳网络平台管理费4元．未来30天，这款时装将开展“每天降价1元”的促销活动，即从第一天起每天的单价均比前一天降1元，通过市场调查发现，该时装单价每降1元，每天销售量增加5件，设第 $x$天 $(1⩽x⩽30$且 $x$为整数）的销量为 $y$件．

（1）直接写出 $y$与 $x$的函数关系式；

（2）在这30天内，哪一天的利润是6300元？

（3）设第 $x$天的利润为 $W$元，试求出 $W$与 $x$之间的函数关系式，并求出哪一天的利润最大，最大利润是多少．

若关于 $x$的方程 $k{x}^2-x-\frac{3}{4}=0$有实数根，则实数 $k$的取值范围是 $($　　 $)$

A． $k=0$B． $k⩾-\frac{1}{3}$且 $k\ne 0$C． $k⩾-\frac{1}{3}$D． $k>-\frac{1}{3}$

小李在景区销售一种旅游纪念品，已知每件进价为6元，当销售单价定为8元时，每天可以销售200件．市场调查反映：销售单价每提高1元，日销量将会减少10件，物价部门规定：销售单价不能超过12元，设该纪念品的销售单价为 $x$（元 $)$，日销量为 $y$（件 $)$，日销售利润为 $w$（元 $)$．

（1）求 $y$与 $x$的函数关系式．

（2）要使日销售利润为720元，销售单价应定为多少元？

（3）求日销售利润 $w$（元 $)$与销售单价 $x$（元 $)$的函数关系式，当 $x$为何值时，日销售利润最大，并求出最大利润．

若关于 $x$的一元二次方程 $a{x}^2-8x+4=0$有两个不相等的实数根，则 $a$的取值范围是　　．

你知道吗，对于一元二次方程，我国古代数学家还研究过其几何解法呢！以方程 $x^2+5x-14=0$ 即 $x(x+5)=14$ 为例加以说明．数学家赵爽（公元 $3~4$ 世纪）在其所著的《勾股圆方图注》中记载的方法是：构造图（如下面左图）中大正方形的面积是 ${(x+x+5)}^2$ ，其中它又等于四个矩形的面积加上中间小正方形的面积，即 $4\times 14+5^2$ ，据此易得 $x=2$ ．那么在下面右边三个构图（矩形的顶点均落在边长为1的小正方形网格格点上）中，能够说明方程 $x^2-4x-12=0$ 的正确构图是 　             　．（只填序号）

已知一元二次方程 $3x^2+4x-k=0$ 有两个不相等的实数根，则 $k$ 的取值范围 　                　．

关于 $x$ 的方程 $2x^2-3x+c=0$ 有两个不相等的实数根，则 $c$ 的取值范围是 　          　．

某企业2018年初获利润300万元，到2020年初计划利润达到507万元．设这两年的年利润平均增长率为 $x$ ．应列方程是 $($ 　　 $)$

A．	$300(1+x)=507$
B．	$300{(1+x)}^2=507$
C．	$300(1+x)+300{(1+x)}^2=507$
D．	$300+300(1+x)+300{(1+x)}^2=507$

若 $2-\sqrt{3}$ 是方程 $x^2-4x+c=0$ 的一个根，则 $c$ 的值是 $($ 　　 $)$

A．

1

B．

$3-\sqrt{3}$

C．

$1+\sqrt{3}$

D．

$2+\sqrt{3}$

关于 $x$ 的一元二次方程 $(a-1)x^2+3x-2=0$ 有实数根，则 $a$ 的取值范围是 $($ 　　 $)$

A．

$a>-\frac{1}{8}$

B．

$a⩾-\frac{1}{8}$

C．

$a>-\frac{1}{8}$ 且 $a\ne 1$

D．

$a⩾-\frac{1}{8}$ 且 $a\ne 1$

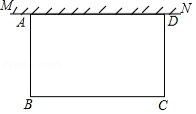
空地上有一段长为 $a$ 米的旧墙 $\mathit{MN}$ ，某人利用旧墙和木栏围成一个矩形菜园 $\mathit{ABCD}$ ，已知木栏总长为100米．

（1）已知 $a=20$ ，矩形菜园的一边靠墙，另三边一共用了100米木栏，且围成的矩形菜园面积为450平方米．如图1，求所利用旧墙 $\mathit{AD}$ 的长；

（2）已知 $0<a<50$ ，且空地足够大，如图2．请你合理利用旧墙及所给木栏设计一个方案，使得所围成的矩形菜园 $\mathit{ABCD}$ 的面积最大，并求面积的最大值．

已知关于 $x$ 的一元二次方程 $(a+1)x^2+2\mathit{bx}+(a+1)=0$ 有两个相等的实数根，下列判断正确的是 $($ 　　 $)$

A．	1一定不是关于 $x$ 的方程 $x^2+\mathit{bx}+a=0$ 的根
B．	0一定不是关于 $x$ 的方程 $x^2+\mathit{bx}+a=0$ 的根
C．	1和 $-1$ 都是关于 $x$ 的方程 $x^2+\mathit{bx}+a=0$ 的根
D．	1和 $-1$ 不都是关于 $x$ 的方程 $x^2+\mathit{bx}+a=0$ 的根

如图，在足够大的空地上有一段长为 $a$ 米的旧墙 $\mathit{MN}$ ，某人利用旧墙和木栏围成一个矩形菜园 $\mathit{ABCD}$ ，其中 $\mathit{AD}⩽\mathit{MN}$ ，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．

（1）若 $a=20$ ，所围成的矩形菜园的面积为450平方米，求所利用旧墙 $\mathit{AD}$ 的长；

（2）求矩形菜园 $\mathit{ABCD}$ 面积的最大值．

已知关于 $x$ 的一元二次方程 $(a+1)x^2+2\mathit{bx}+(a+1)=0$ 有两个相等的实数根，下列判断正确的是 $($ 　　 $)$

A．	1一定不是关于 $x$ 的方程 $x^2+\mathit{bx}+a=0$ 的根
B．	0一定不是关于 $x$ 的方程 $x^2+\mathit{bx}+a=0$ 的根
C．	1和 $-1$ 都是关于 $x$ 的方程 $x^2+\mathit{bx}+a=0$ 的根
D．	1和 $-1$ 不都是关于 $x$ 的方程 $x^2+\mathit{bx}+a=0$ 的根

若关于 $x$的方程 $-2x+m\sqrt{2017-x}+4020=0$存在整数解，则正整数 $m$的所有取值的和为　       　．