将从1开始的自然数按以下规律排列,例如位于第3行、第4列的数是12,则位于第45行、第8列的数是 .

将从1开始的连续自然数按以下规律排列:
第1行 |
1 |
||||||||
第2行 |
2 |
3 |
4 |
||||||
第3行 |
9 |
8 |
7 |
6 |
5 |
||||
第4行 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
||
第5行 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
则2018在第 行.
1261年,我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律,比欧洲的相同发现要早三百多年,我们把这个三角形称为“杨辉三角”,请观察图中的数字排列规律,则 , , 的值分别为

A. , , B. , ,
C. , , D. , ,
我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”从图中取一列数:1,3,6,10, ,记 , , , , ,那么 的值是 .

按一定顺序排列的一列数叫做数列,如数列: , , , , ,则这个数列前2018个数的和为 .
将正整数1至2018按一定规律排列如下表:
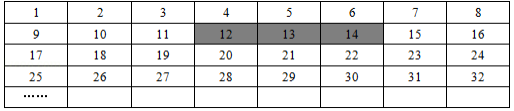
平移表中带阴影的方框,方框中三个数的和可能是
A.2019B.2018C.2016D.2013
我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将 化为分数形式
由于 ,设 ①
则 ②
② ①得 ,解得 ,于是得 .
同理可得 ,
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(基础训练)
(1) , ;
(2)将 化为分数形式,写出推导过程;
(能力提升)
(3) , ;
(注 ,
(探索发现)
(4)①试比较 与1的大小: 1(填“ ”、“ ”或“ ”
②若已知 ,则 .
(注
古希腊数学家把1、3、6、10、15、21、 叫做三角形数,其中1是第一个三角形数,3是第二个三角形数,6是第三个三角形数, ,依此类推,第100个三角形数是 .
如图,是按一定规律排成的三角形数阵,按图中数阵的排列规律,第9行从左至右第5个数是
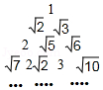
A. B. C. D.
如图所示,是一个运算程序示意图.若第一次输入 的值为125,则第2018次输出的结果是 .

将数1个1,2个 ,3个 , , 个 为正整数)顺次排成一列:1, , ,记 , , , , , , , , ,则 .
小光和小王玩“石头、剪子、布”游戏,规定:一局比赛后,胜者得3分,负者得 分,平局两人都得0分,小光和小王都制订了自己的游戏策略,并且两人都不知道对方的策略.
小光的策略是:石头、剪子、布、石头、剪子、布、
小王的策略是:剪子、随机、剪子、随机 (说明:随机指石头、剪子、布中任意一个)
例如,某次游戏的前9局比赛中,两人当时的策略和得分情况如下表
局数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
小光实际策略 |
石头 |
剪子 |
布 |
石头 |
剪子 |
布 |
石头 |
剪子 |
布 |
小王实际策略 |
剪子 |
布 |
剪子 |
石头 |
剪子 |
剪子 |
剪子 |
石头 |
剪子 |
小光得分 |
3 |
3 |
|
0 |
0 |
|
3 |
|
|
小王得分 |
|
|
3 |
0 |
0 |
3 |
|
3 |
3 |
已知在另一次游戏中,50局比赛后,小光总得分为 分,则小王总得分为 分.
定义:分数 , 为正整数且互为质数)的连分数 (其中 , , , ,为整数,且等式右边的每个分数的分子都为 ,记作 ,
例如: , 的连分数为 ,记作 ,则 .
按照一定规律排列的 个数: 、4、 、16、 、64、 ,若最后三个数的和为768,则 为
A.9B.10C.11D.12