给出下列五个命题:
① 中,
中, 是
是 成立的充要条件;
成立的充要条件;
②当 时,有
时,有 ;
;
③已知 是等差数列
是等差数列 的前n项和,若
的前n项和,若 ,则
,则 ;
;
④若函数 为R上的奇函数,则函数
为R上的奇函数,则函数 的图象一定关于点
的图象一定关于点 成中心对称.
成中心对称.
⑤函数 有最大值为
有最大值为 ,有最小值为0。
,有最小值为0。
其中所有正确命题的序号为 .
凸函数的性质定理:如果函数f(x)在区间D上是凸函数,则对于区间D内的任意x1,x2,…,xn,有 ≤f
≤f ,已知函数y="sin" x在区间(0,π)上是凸函数,则在△ABC中,sin A+sin B+sin C的最大值为 .
,已知函数y="sin" x在区间(0,π)上是凸函数,则在△ABC中,sin A+sin B+sin C的最大值为 .
命题P:实数x满足 其中a<0,命题q:实数x满足
其中a<0,命题q:实数x满足 或
或 且
且 是
是 的必要不充分条件,求a的取值范围
的必要不充分条件,求a的取值范围
(本小题12分)已知 满足
满足 .
.
(1)将 表示为
表示为 的函数
的函数 ,并求
,并求 的单调递增区间;
的单调递增区间;
(2)已知 三个内角
三个内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,若
,若 ,且
,且 ,求
,求 面积的最大值.
面积的最大值.
某航模兴趣小组的同学,为了测定在湖面上航模航行的速度,采用如下办法:在岸边设置两个观察点A、B ,且 AB长为80米,当航模在C处时,测得∠ABC=105°和∠BAC=30°,经过20 秒后,航模直线航行到 D 处,测得 ∠BAD=90°和 ∠ABD=45°.请你根据以上条件求出航模的速度.(答案保留根号)
将一个长宽分别是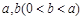 的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,若这个长方体的外接球的体积存在最小值,则
的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,若这个长方体的外接球的体积存在最小值,则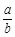 的取值范围是 ▲ .
的取值范围是 ▲ .