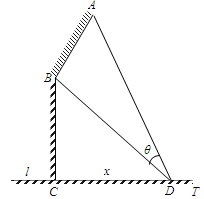
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60o(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4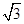 km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
(1)将tanq表示为x的函数;
(2)求点D的位置,使q取得最大值.
在△ABC中,角A,B,C所对边的边长分别是a,b,c.
(1)若c=2,C=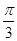 且△ABC的面积等于
且△ABC的面积等于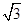 ,求cos(A+B)和a,b的值;
,求cos(A+B)和a,b的值;
(2)若B是钝角,且cos A=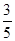 ,sin B=
,sin B=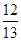 ,求sin C的值.
,求sin C的值.
在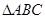 中,角
中,角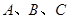 所对的边为
所对的边为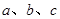 ,且满足
,且满足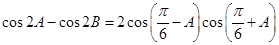
(1)求角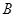 的值;
的值;
(2)若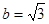 且
且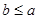 ,求
,求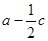 的取值范围.
的取值范围.
已知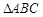 的三内角分别为
的三内角分别为 ,向量
,向量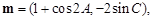
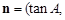
 ,记函数
,记函数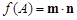 .
.
(1)若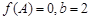 ,求
,求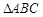 的面积;
的面积;
(2)若关于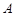 的方程
的方程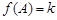 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
已知函数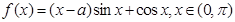 .
.
(1)当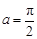 时,求函数
时,求函数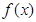 值域;
值域;
(2)当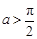 时,求函数
时,求函数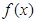 的单调区间.
的单调区间.
命题P:实数x满足 其中a<0,命题q:实数x满足
其中a<0,命题q:实数x满足 或
或 且
且 是
是 的必要不充分条件,求a的取值范围
的必要不充分条件,求a的取值范围
(本小题12分)已知 满足
满足 .
.
(1)将 表示为
表示为 的函数
的函数 ,并求
,并求 的单调递增区间;
的单调递增区间;
(2)已知 三个内角
三个内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,若
,若 ,且
,且 ,求
,求 面积的最大值.
面积的最大值.
某航模兴趣小组的同学,为了测定在湖面上航模航行的速度,采用如下办法:在岸边设置两个观察点A、B ,且 AB长为80米,当航模在C处时,测得∠ABC=105°和∠BAC=30°,经过20 秒后,航模直线航行到 D 处,测得 ∠BAD=90°和 ∠ABD=45°.请你根据以上条件求出航模的速度.(答案保留根号)