在4次独立试验中,事件A出现的概率相同,若事件A至少发生1次的概率是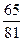 ,则事件A 在一次试验中出现的概率是( )
,则事件A 在一次试验中出现的概率是( ) 12
12
A.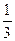 |
B.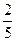 |
C.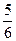 |
D. |
一射手对同一目标独立地射击4次,若至少命中一次的概率为 ,则该射手一次射击的命中率为 ________________________
,则该射手一次射击的命中率为 ________________________
某地举行篮球比赛,其中男子篮球总决赛在雄风队与豪杰队之间角逐,采用七局四胜制,若有一队胜4场,由此队获胜且结束比赛,因而队实力非常接近,在每场比赛中两队获胜是等可能的。据以往资料统计,每场比赛组织者可获门票收入5万元,两队决出胜负后,问:
(1)求组织者在此次决赛中获门票收入为20万元的概率。
(2)求组织者在此次决赛中获门票收入不少于30万元的概率。
(1)门票收入20万无,必须比赛四场,且能决出胜负
某车间在三天内,每天生产10件某产品,其中第一天,第二天分别生产出了1件、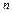 件次品,而质检部每天要从生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过。则第一天通过检查的概率 ; 若
件次品,而质检部每天要从生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过。则第一天通过检查的概率 ; 若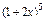 的第三项的二项式系数为
的第三项的二项式系数为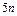 ,则第二天通过检查的概率
,则第二天通过检查的概率
某一批花生种子,如果每 粒发芽的概率为 ,那么播下 粒种子恰有 粒发芽的概率是()
| A. | B. | C. | D. |
某单位为绿化环境,移栽了甲、乙两种大树各2株。设甲、乙两种大树移栽的成活率分别为
和
,且各株大树是否成活互不影响。求移栽的4株大树中:
(Ⅰ)至少有1株成活的概率;
(Ⅱ)两种大树各成活1株的概率。
甲、乙两人各射击一次,击中目标的概率分别是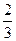 和
和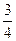 .假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
(Ⅰ)求甲射击4次,至少1次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(Ⅲ)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?
甲、乙两支足球队,苦战120分钟,比分为1 :1,现决定各派5名队员,每人射一个点球决定胜负,假设两支球队派出的队员点球命中率均为
⑴两队球员一个间隔一个出场射球,有多少种不同的出场顺序?
⑵甲、乙两队各射完5个点球后,再次出现平局的概率是多少?