从10个元件中(其中4个相同的甲品牌元件和6个相同的乙品牌元件)随机选出3个参加某种性能测试. 每个甲品牌元件能通过测试的概率均为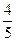 ,每个乙品牌元件能通过测试的概率均为
,每个乙品牌元件能通过测试的概率均为 .试求:
.试求:
(I)选出的3个元件中,至少有一个甲品牌元件的概率;
(II)若选出的三个元件均为乙品牌元件,现对它们进行性能测试,求至少有两个乙品牌元件同时通过测试的概率.
相关知识点
推荐套卷
从10个元件中(其中4个相同的甲品牌元件和6个相同的乙品牌元件)随机选出3个参加某种性能测试. 每个甲品牌元件能通过测试的概率均为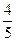 ,每个乙品牌元件能通过测试的概率均为
,每个乙品牌元件能通过测试的概率均为 .试求:
.试求:
(I)选出的3个元件中,至少有一个甲品牌元件的概率;
(II)若选出的三个元件均为乙品牌元件,现对它们进行性能测试,求至少有两个乙品牌元件同时通过测试的概率.