某大学对该校参加某项活动的志愿者实施“社会教育实施”学分考核,该大学考核只有合格和优秀两个等次.若某志愿者考核为合格,授予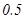 个学分;考核为优秀,授予
个学分;考核为优秀,授予 个学分.假设该校志愿者甲、乙考核为优秀的概率分别为
个学分.假设该校志愿者甲、乙考核为优秀的概率分别为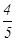 、
、 ,乙考核合格且丙考核优秀的概率为
,乙考核合格且丙考核优秀的概率为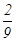 .甲、乙、丙三人考核所得等次相互独立.
.甲、乙、丙三人考核所得等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中,甲、乙、丙三名志愿者所得学分之和为随机变量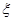 ,求随机变量
,求随机变量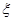 的
的
分布列和数学期望.
推荐套卷
某大学对该校参加某项活动的志愿者实施“社会教育实施”学分考核,该大学考核只有合格和优秀两个等次.若某志愿者考核为合格,授予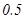 个学分;考核为优秀,授予
个学分;考核为优秀,授予 个学分.假设该校志愿者甲、乙考核为优秀的概率分别为
个学分.假设该校志愿者甲、乙考核为优秀的概率分别为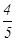 、
、 ,乙考核合格且丙考核优秀的概率为
,乙考核合格且丙考核优秀的概率为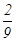 .甲、乙、丙三人考核所得等次相互独立.
.甲、乙、丙三人考核所得等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中,甲、乙、丙三名志愿者所得学分之和为随机变量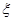 ,求随机变量
,求随机变量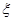 的
的
分布列和数学期望.