10.一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了ξ次球,则P(ξ=12)等于
A.C ( ( )10·( )10·( )2 )2 |
B.C ( ( )9( )9( )2· )2· |
C.C ( ( )9·( )9·( )2 )2 |
D.C ( ( )9·( )9·( )2 )2 |
设导弹发射的事故率为0.01,若发射10次,其出事故的次数为ξ,则下列结论正确的是( )
| A.Eξ="0.1" | B.Dξ="0.1" |
| C.P(ξ=k)=0.01k·0.9910-k | D.P(ξ=k)=C ·0.99k·0.0110-k ·0.99k·0.0110-k |
某气象站天气预报的准确率为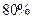 ,计算(结果保留到小数点后面第2位)
,计算(结果保留到小数点后面第2位)
(1)5次预报中恰有2次准确的概率;
(2)5次预报中至少有2次准确的概率;
甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即以先赢2局者为胜.根据经验,每局比赛中甲获胜的概率为0.6,则本次比赛甲获胜的概率是
A 0.216 B0.36 C0.432 D0.648
口袋里放有大小相等的两个红球和一个白球,有放回地每次摸取一个球,数列 满足:
满足: 如果
如果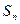 为数列
为数列 的前n项和,那么
的前n项和,那么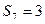 的概率为 ( )
的概率为 ( )
A.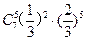 |
B.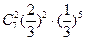 |
C. |
D.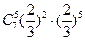 |
甲,乙两人进行乒兵球比赛,在每一局比赛中,甲获胜的概率为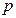 。
。
(1)如果甲,乙两人共比赛4局,甲恰好负2局的概率不大于其恰好胜3局的概率,试求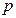 的取值范围;
的取值范围;
(2)若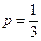 ,当采用3局2胜制的比赛规则时,求甲获胜的概率;
,当采用3局2胜制的比赛规则时,求甲获胜的概率;
(3)如果甲,乙两人比赛6局,那么甲恰好胜3局的概率可能是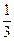 吗?
吗?
甲、乙两个篮球运动员相互没有影 响地站在罚球线上投球,其中甲的命中率为
响地站在罚球线上投球,其中甲的命中率为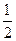 ,乙的命中率为
,乙的命中率为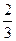 ,现在每人都投球三次,且各次投球的结果互不影响.求:
,现在每人都投球三次,且各次投球的结果互不影响.求:
(1)甲恰好投进两球 的概率
的概率 ;
;
(2)甲乙两人都恰好投进两球的概率;
有一批食品出厂前要进行五项指标检验,如果有两项指标不合格,则这批食品不能出厂.已知每项指标抽检是相互独立的,且每项抽检出现不合格的概率都是 .
.
(1)求这批产品不能出厂的概率(保留三位有效数字);
(2)求直至五项指标全部验完毕,才能确定该批食品是否出厂的概率(保留三位有效数字).
高三(1)班、高三(2)班每班已选出3名学生组成代表队,进行乒乓球对抗赛. 比赛规则是:①按“单打、双打、单打”顺序进行三盘比赛;②代表队中每名队员至少参加一盘比赛,不得参加两盘单打比赛. 已知每盘比赛双方胜出的概率均为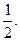
(Ⅰ)根据比赛规则,高三(1)班代表队共可排出多少种不同的出场阵容?
(Ⅱ)高三(1)班代表队连胜两盘的概率是多少?