（本小题满分14分）甲、乙两人进行乒乓球单打比赛，采用五局三胜制（即先胜三局者获冠军）．对于每局比赛，甲获胜的概率为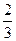
，乙获胜的概率为
．如果将“乙获得冠军”的事件称为“爆出冷门”．试求此项赛事爆出冷门的概率．
相关试题
中，
平面
，
，
，
为
的中点，
.
与
所成角的大小；
平面
；
与平面
，直线
.
与圆
恒相交；
的值以及最短弦长.
中，
，
，且
、
分别是
、
的中点.
面
；（2）面
面
.
向圆
作切线，求切线的方程；
在圆
上，点
在直线
上，求
的最小值.
中，已知棱
的长为
，其余各棱长都为1，求二面角
的大小.相关知识点
推荐套卷
（本小题满分14分）甲、乙两人进行乒乓球单打比赛，采用五局三胜制（即先胜三局者获冠军）．对于每局比赛，甲获胜的概率为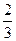，乙获胜的概率为．如果将“乙获得冠军”的事件称为“爆出冷门”．试求此项赛事爆出冷门的概率．
粤公网安备 44130202000953号