[江苏]2012届江苏省南京市高三年级学情调研卷数学
某工厂生产某种产品5000件,它们来自甲、乙、丙3条不同的生产线.为检查这批产品的质量,决定采用分层抽样的方法进行抽样.若从甲、乙、丙三条生产线抽取的件数之比为1:2:2,则乙生产线 生产了 ▲ 件产品
生产了 ▲ 件产品
已知抛物线y2=4x的焦点为F,准线为l.过点F作倾斜角为60°的直线与抛物线在第一象限的交点为A,过A作l的垂线,垂足为A1,则△AA1F的面积是 ▲
在平面直角坐标系xOy中,若直线y=kx+1与曲线y=∣x+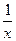 ∣-∣x-
∣-∣x-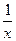 ∣有四个公共点,则实数k的取值范围是 ▲ .
∣有四个公共点,则实数k的取值范围是 ▲ .
(本小题满 分14分)已知函数f(x)=2
分14分)已知函数f(x)=2 sinxco
sinxco sx-2sin2x.
sx-2sin2x.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[- ,
, ]上的最大值和最小值.
]上的最大值和最小值.
(本小题满分14分)如图,在直三棱柱ABC-A1B1C1中,点D、E分别在边BC、
B1C1上,CD=B1E=AC,ÐA CD=60°.
CD=60°.
求证:(1)BE∥平面AC1D;
(2) 平面ADC1⊥平面BCC1B1.
平面ADC1⊥平面BCC1B1.

(本小题满分14分)如图,在平面直角坐标系xOy中,椭圆C的中心在坐标原点O,右焦点为F.若C的右准线l的方程为x=4,离心率e=.
(1)求椭圆C的标准方程;
(2)设点P为直线l上一动点,且 在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
(本小题满分16分)经销商用一辆J型卡车将某种水果从果园运送(满载)到相距400km的水果批发市场.据测算,J型卡车满载行驶时,每100km所消耗的燃油量u(单位: 资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
(1)设运送这车水果 的费用为y(元)(不计返程费用),将y表示成速度v的函数
的费用为y(元)(不计返程费用),将y表示成速度v的函数 关系式;
关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
(本小题满分16分)已知函数f(x)=x2-(1+2a)x+alnx(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
(本小题满分16分)设等差数列{an}的前n项和是Sn,已知S3=9,S6=36.
(1)求数列{an}的通项公式;
(2)是否存在正整数m、k,使am,am+5,ak成等比数列?若存在,求出m和k的值,若不存在,说明理 由;
由;
(3)设数列{bn}的通项公式为bn=3n-2.集合A={x∣x=an,n∈N*},B={x∣x=bn,n∈N*}.将集合A∪B中的元素从小到大依次排列,构成数列c1,c2,c3 ,
, …,求{cn}的通项公式.
…,求{cn}的通项公式.
选修4—1:几何证明选讲如图,AB为圆O的直径,D为圆O上一点,过D作圆O的切线交AB的延长线于点C,若DA=DC,求证:AB=2BC.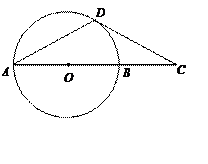
选修4— 4:坐标系与参数方程
4:坐标系与参数方程
在极坐标系中,已知直线l:rcos(q+)=,圆C:r=4cosq,求直线l被圆C截得的弦长.
一个口袋中装有大小和质地都相同的白球和红球共7个, 其中白球个数不少于红球个数.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为随机变量X.若P(X=2)=
其中白球个数不少于红球个数.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为随机变量X.若P(X=2)= .
.
(1)求口袋中的白球个数;
(2)求 X的概率分布与数学期望.
X的概率分布与数学期望.
 复数z的模是 ▲ .
复数z的模是 ▲ . 分别为2,3,4,5,现从中任取三条,则以这三条线段为边可以构成三角形的概率是 ▲
分别为2,3,4,5,现从中任取三条,则以这三条线段为边可以构成三角形的概率是 ▲ 
 的定义域为集合A,则集合A∩Z中元素的个数是 ▲ .
的定义域为集合A,则集合A∩Z中元素的个数是 ▲ . ,则f(-4)的值是 ▲ .
,则f(-4)的值是 ▲ . ▲ .
▲ . ,a4=-4,则| a1|+| a2|+…+| a
,a4=-4,则| a1|+| a2|+…+| a 6|= ▲ .
6|= ▲ . ,则向量a,b的夹角等于 ▲
,则向量a,b的夹角等于 ▲ 
 B1D^平面PQR;
B1D^平面PQR;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号