(本小题满分16分)设等差数列{an}的前n项和是Sn,已知S3=9,S6=36.
(1)求数列{an}的通项公式;
(2)是否存在正整数m、k,使am,am+5,ak成等比数列?若存在,求出m和k的值,若不存在,说明理 由;
由;
(3)设数列{bn}的通项公式为bn=3n-2.集合A={x∣x=an,n∈N*},B={x∣x=bn,n∈N*}.将集合A∪B中的元素从小到大依次排列,构成数列c1,c2,c3 ,
, …,求{cn}的通项公式.
…,求{cn}的通项公式.
相关知识点
推荐套卷
 元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金. Pn(b).
Pn(b).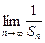 ,其中Sn=b1+b2+…+bn;
,其中Sn=b1+b2+…+bn;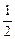 ,求数列{
,求数列{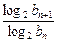 }的最大项和最小项的值.
}的最大项和最小项的值.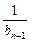 )(n=2,3,4…),求数列{bn}的通项bn;
)(n=2,3,4…),求数列{bn}的通项bn; )(其中a>0且a≠1),记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1),记Sn是数列{an}的前n项和,试比较Sn与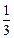 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论. 粤公网安备 44130202000953号
粤公网安备 44130202000953号