函数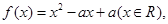 数列
数列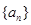 的前
的前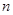 项和
项和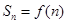 ,且
,且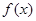 同时满足:①不等式
同时满足:①不等式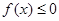 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在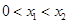 ,使得不等式
,使得不等式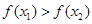 成立.
成立.
(1)求函数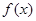 的表达式;
的表达式;
(2)求数列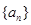 的通项公式.
的通项公式.
在数列{an}中,an+1=an+a(n∈N*,a为常数),若平面上的三个不共线的非零向量 满足
满足 ,三点A,B,C共线且该直线不过O点,则S2010等于()
,三点A,B,C共线且该直线不过O点,则S2010等于()
| A.1005 | B.1006 | C.2010 | D.2012 |
已知数列: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,…,依它的前10项的规律,这个数列的第2 013项a2 013满足()
,…,依它的前10项的规律,这个数列的第2 013项a2 013满足()
A.0<a2 013< |
B. ≤a2 013<1 ≤a2 013<1 |
| C.1≤a2 013≤10 | D.a2 013>10 |
已知数列 中
中 ,函数
,函数 .
.
(1)若正项数列 满足
满足 ,试求出
,试求出 ,
, ,
, ,由此归纳出通项
,由此归纳出通项 ,并加以证明;
,并加以证明;
(2)若正项数列 满足
满足 (n∈N*),数列
(n∈N*),数列 的前项和为Tn,且
的前项和为Tn,且 ,求证:
,求证: .
.