全国重点高中提前招生真题过关(十五)
由四个全等的直角三角形和一个小正方形组成的大正方形 如图所示.过点 作 的垂线交小正方形对角线 的延长线于点 ,连接 ,延长 交 于点 .若 ,则 的值为 ( )

| A. |
|
B. |
|
C. |
|
D. |
|
有一块锐角三角形余料 ,它的边 边上的高为 ,现要把它分割成若干个邻边长分别为 和 的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小长方形的长为 的边在 上,则按如图方式分割成的小长方形零件最多有 ( )

| A. |
个 |
B. |
个 |
C. |
个 |
D. |
个 |
如图,有一块锐角三角形材料,边 ,高 ,要把它加工成矩形零件,使其一边在 上,其余两个顶点分别在 上,且 ,则这个矩形零件的长为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 和 表示两根直立于地面的柱子, 和 表示起固定作用的两根钢筋, 与 相交于点 ,已知 ,则点 离地面的高度 为( )

| A. |
|
B. |
|
C. |
|
D. |
|
已知抛物线 的顶点为 ,点 是第一象限内该二次函数图象上一点,过点 作 轴的平行线交二次函数图象于点 ,分别过点 作 轴的垂线,垂足分别为 ,连接 交 于点 与 ( )

| A. |
始终不相似 |
B. |
始终相似 |
| C. |
只有 时相似 |
D. |
无法确定 |
如图所示, 是 的中位线, 为 上一点,且 的延长线交 于点 的延长线交 于点 ,则 等于( )

| A. |
|
B. |
|
C. |
|
D. |
|
抛物线 的一部分如图所示,设该抛物线与 轴的交点为 和 ,与 轴的交点为 ,若 ,则 的值为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,正方形 中,点 是 边上一点,连接 ,以 为对角线作正方形 ,边 与正方形 的对角线 相交于点 ,连接 ,有以下五个结论:① ;② ;③ ;④ ;⑤若 ,则 .你认为其中正确的结论是_____(填写序号).

如图①,在 中, ,边 上的点 从顶点 出发,向顶点 运动,同时,边 上的点 从顶点 出发,向顶点 运动, 两点运动速度的大小相等.设 关于 的函数图象如图②,图象过点 ,则图象最低点的横坐标是_____.

一个铝质三角形框架三条边长分别为 ,要做一个与它相似的铝质三角形框架,现有长为 的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边,截法有_____种.
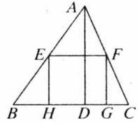
如图,正方形 内接于 ,设 表示一个两位数 ,三角形高 ,已知 恰好是从小到大的四个连续正整数,则 的面积为_____.
如图,在四边形 中, 是对角线 的中点,连接 并延长交边 于点 .
(1)当点 在 上,①求证: ;②若 ,求 的值;
(2)若 ,求 的长.

如图,在平面直角坐标系 中,抛物线 与两坐标轴分别相交于 三点.
(1)求证: ;
(2)点 是第一象限内该抛物线上的动点,过点 作 轴的垂线交 于点 ,交 轴于点 .
①求 的最大值;
②点 是 的中点,若以点 为顶点的三角形与 相似,求点 的坐标.

如图,点 在以 为直径的 上,过 作 的切线交 的延长线于点 于点 ,交 于点 ,连接 .
(1)求证:
(2)求证: ;
(3)若 ,求 的长.

如图,开口向下的抛物线 与 轴交于 两点,抛物线上另有一点 在第一象限,且使 .
(1)求 的长及 的值;
(2)设直线 与 轴交于 点,点 是 的中点时,求直线 和抛物线的解析式.

图1是一种手机托架,使用该手机托架示意图如图3所示,底部放置手机处宽 ,托架斜面长 ,它有 到 共4个挡位调节角度,相邻两个挡位间的距离为 ,挡位 到 的距离为 .将某型号手机置于托架上(图2,手机屏幕长 是 , 是支点且 (支架的厚度忽略不计).求:
(1)当支架调到 挡时,点 离水平面的距离 为多少厘米;
(2)当支架从 挡调到 挡时,点 离水平面的距离下降了多少厘米.








 粤公网安备 44130202000953号
粤公网安备 44130202000953号