图1是一种手机托架,使用该手机托架示意图如图3所示,底部放置手机处宽 ,托架斜面长 ,它有 到 共4个挡位调节角度,相邻两个挡位间的距离为 ,挡位 到 的距离为 .将某型号手机置于托架上(图2,手机屏幕长 是 , 是支点且 (支架的厚度忽略不计).求:
(1)当支架调到 挡时,点 离水平面的距离 为多少厘米;
(2)当支架从 挡调到 挡时,点 离水平面的距离下降了多少厘米.
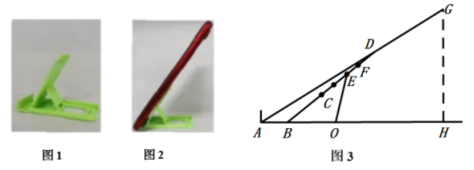
图1是一种手机托架,使用该手机托架示意图如图3所示,底部放置手机处宽 ,托架斜面长 ,它有 到 共4个挡位调节角度,相邻两个挡位间的距离为 ,挡位 到 的距离为 .将某型号手机置于托架上(图2,手机屏幕长 是 , 是支点且 (支架的厚度忽略不计).求:
(1)当支架调到 挡时,点 离水平面的距离 为多少厘米;
(2)当支架从 挡调到 挡时,点 离水平面的距离下降了多少厘米.
