在△ABC中,设AD为BC边上的高,且AD = BC,b,c分别表示角B,C所对的边长,则 的取值范围是_______ .
的取值范围是_______ .
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60o(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4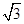 km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
(1)将tanq表示为x的函数;
(2)求点D的位置,使q取得最大值.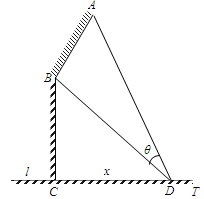
安徽高考设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,3sin A=5sin B,则角C=( )
A.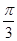 |
B. |
C.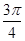 |
D.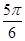 |
在△ABC中,角A,B,C所对边的边长分别是a,b,c.
(1)若c=2,C=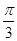 且△ABC的面积等于
且△ABC的面积等于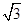 ,求cos(A+B)和a,b的值;
,求cos(A+B)和a,b的值;
(2)若B是钝角,且cos A=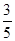 ,sin B=
,sin B=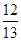 ,求sin C的值.
,求sin C的值.
在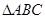 中,角
中,角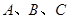 所对的边为
所对的边为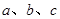 ,且满足
,且满足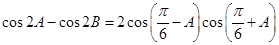
(1)求角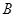 的值;
的值;
(2)若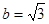 且
且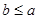 ,求
,求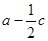 的取值范围.
的取值范围.
已知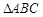 的三内角分别为
的三内角分别为 ,向量
,向量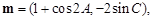
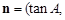
 ,记函数
,记函数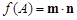 .
.
(1)若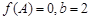 ,求
,求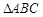 的面积;
的面积;
(2)若关于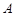 的方程
的方程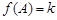 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
已知函数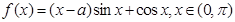 .
.
(1)当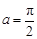 时,求函数
时,求函数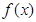 值域;
值域;
(2)当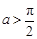 时,求函数
时,求函数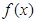 的单调区间.
的单调区间.
若在△ABC中,有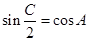 ,则△ABC一定是 ()
,则△ABC一定是 ()
| A.锐角三角形 | B.钝角三角形 | C.直角三角形 | D.等腰三角形 |
在 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、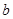 、
、 ,
,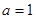 ,
, ,当
,当 的面积等于
的面积等于 时,
时, _______________.
_______________.