高中数学随机事件试题

设甲、乙两位同学上学期间，每天7：30之前到校的概率均为 $\frac{2}{3}$．假定甲、乙两位同学到校情况互不影响，且任一同学每天到校情况相互独立．

（Ⅰ）用 $X$表示甲同学上学期间的三天中7：30之前到校的天数，求随机变量 $X$的分布列和数学期望；

（Ⅱ）设 $M$为事件“上学期间的三天中，甲同学在7：30之前到校的天数比乙同学在7：30之前到校的天数恰好多2”，求事件 $M$发生的概率．

改革开放以来，人们的支付方式发生了巨大转变．近年来，移动支付已成为主要支付方式之一．为了解某校学生上个月A，B两种移动支付方式的使用情况，从全校所有的1000名学生中随机抽取了100人，发现样本中A，B两种支付方式都不使用的有5人，样本中仅使用A和仅使用B的学生的支付金额分布情况如下：

支付金额 支付方式	不大于 $2000$ 元	大于 $2000$ 元
仅使用A	27人	3人
仅使用B	24人	1人

（Ⅰ）估计该校学生中上个月A，B两种支付方式都使用的人数；

（Ⅱ）从样本仅使用B的学生中随机抽取1人，求该学生上个月支付金额大于 $2000$ 元的概率；

（Ⅲ）已知上个月样本学生的支付方式在本月没有变化．现从样本仅使用B的学生中随机抽查1人，发现他本月的支付金额大于 $2000$ 元．结合（Ⅱ）的结果，能否认为样本仅使用B的学生中本月支付金额大于 $2000$ 元的人数有变化？说明理由．

从个同类产品（其中个是正品，个是次品）中任意抽取个的必然事件是（）

A．个都是正品	B．至少有个是次品
C．个都是次品	D．至少有个是正品

袋中装有3个黑球、2个白球、1个红球，从中任取两个，互斥而不对立的事件是（）

A．“至少有一个黑球”和“没有黑球”

B．“至少有一个白球”和“至少有一个红球”

C．“至少有一个白球”和“红球黑球各有一个”

D．“恰有一个白球”和“恰有一个黑球”

从装有红球、白球和黑球各2个的口袋内一次取出2个球，则与事件“两球都为白球”互斥而非对立的事件是以下事件“①两球都不是白球；②两球恰有一白球；③两球至少有一个白球”中的哪几个？（）

A．①②

B．①③

C．②③

D．①②③

从装有红球、白球和黑球各2个的口袋内一次取出2个球，则与事件“两球都为白球”互斥而非对立的事件是以下事件“①两球都不是白球；②两球恰有一白球；③两球至少有一个白球”中的哪几个？（）

A．①②

B．①③

C．②③

D．①②③

从装有个红球和个黒球的口袋内任取个球，则互斥而不对立的两个事件是（）

A．至少有一个黒球与都是黒球

B．至少有一个黒球与都是红球

C．至少有一个黒球与至少有个红球

D．恰有个黒球与恰有个黒球

从装有红球、黑球和白球的口袋中摸出一个球，若摸出的球是红球的概率是0.4，摸出的球是黑球的概率是0.25，那么摸出的球是白球或黑球的概率是（）

A．0.35

B．0.65

C．0.1

D．0.6

有5件产品，其中3件正品，2件次品，从中任取2件，则互斥而不对立的两个事件是（）

A．至少有1件次品与至多有1件正品

B．至少有1件次品与都是正品

C．至少有1件次品与至少有1件正品

D．恰有1件次品与恰有2件正品

下列四个命题：
①样本方差反映的是所有样本数据与样本平均值的偏离程度；
②某只股票经历了l0个跌停（每次跌停，即下跌l0%）后需再经过10个涨停（每次涨停，即上涨10%）
就可以回到原来的净值；
③某校高三一级部和二级部的人数分别是m、n，本次期末考试两级部；数学平均分分别是a、b，则这两
个级部的数学平均分为
④某中学采用系统抽样方法，从该校高一年级全体800名学生中抽50名学生做牙齿健康检查，现将800
名学生从001到800进行编号，已知从497--512这16个数中取得的学生编号是503，则初始在第1小组
00l～016中随机抽到的学生编号是007．
其中真命题的个数是（）

A．0个

B．1个

C．2个

D．3个

若P（A∪B）=P（A）+P（B）=1，则事件A与B的关系是（）
A．互斥不对立 B．对立不互斥 C．互斥且对立 D．以上都不对

下列说法正确的是（）

A．某厂一批产品的次品率为，则任意抽取其中10件产品一定会发现一件次品

B．气象部门预报明天下雨的概率是90%，说明明天该地区90%的地方要下雨，其余10%的地方不会下雨

C．某医院治疗一种疾病的治愈率为10%，那么前9个病人都没有治愈，第10个人就一定能治愈

D．掷一枚硬币，连续出现5次正面向上，第六次出现反面向上的概率与正面向上的概率仍然都为0．5

甲，乙两队进行排球决赛，现在的情形是甲队只要再赢一局就获冠军，乙队需要再赢两局才能得冠军，若两队胜每局的概率相同，则甲队获得冠军的概率为（）

A．

B．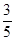

C．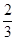

D．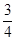

从装有两个红球和两个黑球的口袋内任取两个球，那么互斥而不对立的两个事件是（）

A．“至少有一个黑球”与“都是黑球”

B．“恰有一个黑球”与“恰有两个黑球”

C．“至少有一个黑球”与“至少有一个红球”

D．“至少有一个黑球”与“都是红球”

从12个同类产品（其中有10个正品，2个次品）中，任意抽取3个的必然事件是（）

A．3个都是正品	B．至少有1个次品
C．3个都是次品	D．至少有1个正品