如图,点 在抛物线 上,且在 的对称轴右侧.
(1)写出 的对称轴和 的最大值,并求 的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点 及 的一段,分别记为 .平移该胶片,使 所在抛物线对应的函数恰为 .求点 移动的最短路程.

发现两个已知正整数之和与这两个正整数之差的平方和一定是偶数,且该偶数的一半也可以表示为两个正整数的平方和.
验证 如, 为偶数.请把 的一半表示为两个正整数的平方和;
探究 设“发现”中的两个已知正整数为 ,请论证“发现”中的结论正确.
某公司要在甲、乙两人中招聘一名职员,对两人的学历,能力、经验这三项进行了测试.各项满分均为 分,成绩高者被录用.图1是甲、乙测试成绩的条形统计图,
(1)分别求出甲、乙三项成绩之和,并指出会录用谁;
(2)若将甲、乙的三项测试成绩,按照扇形统计图(图2)各项所占之比,分别计算两人各自的综合成绩,并判断是否会改变(1)的录用结果.

如图,棋盘旁有甲、乙两个围棋盒.
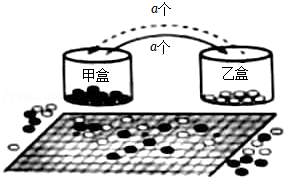
(1)甲盒中都是黑子,共 个.乙盒中都是白子,共 个.嘉嘉从甲盒拿出 个黑子放入乙盒,使乙盒棋子总数是甲盒所剩棋子数的 倍,则 _____;
(2)设甲盒中都是黑子,共 个,乙盒中都是白子,共 个.嘉嘉从甲盒拿出 个黑子放入乙盒中,此时乙盒棋子总数比甲盒所剩棋子数多_____个;接下来,嘉嘉又从乙盒拿回 个棋子放到甲盒,其中含有 个白子,此时乙盒中有 个黑子,则 的值为_____.
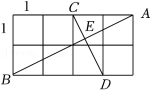
如图是钉板示意图,每相邻 个钉点是边长为 个单位长的小正方形顶点,钉点 的连线与钉点 的连线交于点 ,则
(1) 与 是否垂直?_____(填“是”或“否”);
(2) _____.
如图,某校运会百米预赛用抽签方式确定赛道.若琪琪第一个抽签,她从 号中随机抽取一签,则抽到 号赛道的概率是_____.

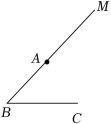
题目:“如图, , ,在射线 上取一点 ,设 ,若对于 的一个数值,只能作出唯一一个 ,求 的取值范围.”对于其答案,甲答: ,乙答: ,丙答: ,则正确的是( )
| A. |
只有甲答的对 |
| B. |
甲、丙答案合在一起才完整 |
| C. |
甲、乙答案合在一起才完整 |
| D. |
三人答案合在一起才完整 |
“曹冲称象”是流传很广的故事,如图.按照他的方法:先将象牵到大船上,并在船侧面标记水位,再将象牵出.然后往船上抬入 块等重的条形石,并在船上留 个搬运工,这时水位恰好到达标记位置,如果再抬入 块同样的条形石,船上只留 个搬运工,水位也恰好到达标记位置.已知搬运工体重均为 斤,设每块条形石的重量是 斤,则正确的是( )

| A. |
依题意 |
| B. |
依题意 |
| C. |
该象的重量是 斤 |
| D. |
每块条形石的重量是 斤 |
五名同学捐款数分别是 (单位:元),捐 元的同学后来又追加了 元.追加后的 个数据与之前的 个数据相比,集中趋势相同的是( )
| A. |
只有平均数 |
B. |
只有中位数 |
| C. |
只有众数 |
D. |
中位数和众数 |
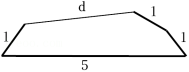
平面内,将长分别为 的线段,顺次首尾相接组成凸五边形(如图),则 可能是( )
| A. |
|
B. |
|
C. |
|
D. |
|
某项工作,已知每人每天完成的工作量相同,且一个人完成需 天.若 个人共同完成需 天,选取 组数对 ,在坐标系中进行描点,则正确的是( )
| A. |
|
| B. |
|
| C. |
|
| D. |
|
要得知作业纸上两相交直线 所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图1和图2):
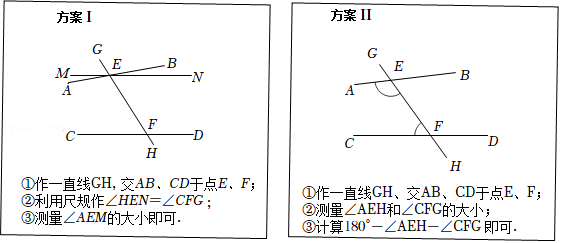
对于方案Ⅰ、Ⅱ,说法正确的是( )
| A. |
Ⅰ可行、Ⅱ不可行 |
B. |
Ⅰ不可行、Ⅱ可行 |
| C. |
Ⅰ、Ⅱ都可行 |
D. |
Ⅰ、Ⅱ都不可行 |
某款“不倒翁”(图1)的主视图是图2, 分别与 所在圆相切于点 .若该圆半径是 , ,则 的长是( )
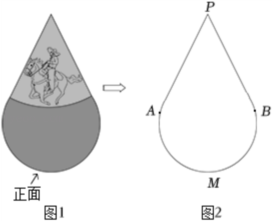
| A. |
|
B. |
|
C. |
|
D. |
|