初中数学填空题

如图，菱形纸片ABCD中，∠A=60°，将纸片折叠，点A、D分别落在A′、D′处，且A′D′经过B，EF为折痕，当D′F⊥CD时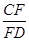，的值为    ．

对正方形ABCD进行分割，如图1，其中E、F分别是BC、CD的中点，M、N、G分别是OB、OD、EF的中点，沿分化线可以剪出一副“七巧板”，用这些部件可以拼出很多图案，图2就是用其中6块拼出的“飞机”．若△GOM的面积为1，则“飞机”的面积为     ．

如图，小红站在水平面上的点A处，测得旗杆BC顶点C的仰角为60°，点A到旗杆的水平距离为a米．若小红的水平视线与地面的距离为b米，则旗杆BC的长为________米。（用含有a、b的式子表示）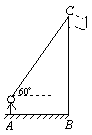

如图，在平面直角坐标系中，抛物线y=（x-2）²与x轴交于点A，与y轴交于点B．过点B作BC∥x轴，交抛物线于点C，过点A作AD∥y轴，交BC于点D，点P在BC下方的抛物线上（P不与B，C重合），连结PC，PD，则△PCD面积的最大值是              ．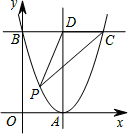

在求1+6+6²+6³+6⁴+6⁵+6⁶+6⁷+6⁸+6⁹的值时，小林发现：从第二个加数起每一个加数都是前一个加数的6倍，于是她设：
S=1+6+6²+6³+6⁴+6⁵+6⁶+6⁷+6⁸+6⁹①
然后在①式的两边都乘以6，得：
6S=6+6²+6³+6⁴+6⁵+6⁶+6⁷+6⁸+6⁹+6¹⁰②②-①得6S-S=6¹⁰-1，即5S=6¹⁰-1，所以S=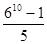，得出答案后，爱动脑筋的小林想：如果把“6”换成字母“a”（a≠0且a≠1），能否求出1+a+a²+a³+a⁴+…+a²⁰¹⁵的值？你的答案是                    ．

在一次数学游戏中，老师在三个盘子里分别放了一些糖果，糖果数依次为，，，记为（，，）．游戏规则如下：若三个盘子中的糖果数不完全相同，则从糖果数最多的一个盘子中拿出两个，给另外两个盘子各放一个（若有两个盘子中的糖果数相同，且都多于第三个盘子中的糖果数，则从这两个盘子字母序在前的盘子中取糖果），记为一次操作．若三个盘子中的糖果数都相同，游戏结束．次操作后的糖果数记为（，，）．小明发现：若（4，8，18），则游戏永远无法结束，那么     ．

在Rt△ABC中，∠C=90°，BC=3，AC=4，点P在以C为圆心，5为半径的圆上，连结PA，PB。若PB=4，则PA的长为   ．

如图，已知直线y=﹣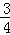x+3分别交x轴、y轴于点A、B，P是抛物线y=﹣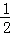x²+2x+5的一个动点，其横坐标为a，过点P且平行于y轴的直线交直线y=﹣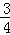x+3于点Q，则当PQ=BQ时，a的值是       ．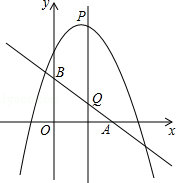

已知，正六边形ABCDEF在直角坐标系内的位置如图所示，A（﹣2，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2015次翻转之后，点B的坐标是      ．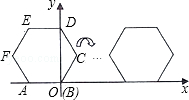

如图1，在正方形ABCD中，延长BC至M，使BM=DN，连接MN交BD延长线于点E．

（1）求证：BD+2DE=BM ．
（2）如图2，连接BN交AD于点F，连接MF交BD于点G．若AF:FD=1:2，且CM=2，则线段DG=_______．

有正面分别标有数字、、、、的五张不透明卡片，它们除数字不同外其余全部相同，现将它们背面朝上，洗匀后从中任取一张，将卡片上的数字记为，则使关于的方程+x－m=0有实数解且关于的不等式组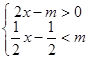有整数解的的概率为    ．

．如图，△ABC、△DCE、△GEF都是正三角形，且B、C、E、F在同一直线上，A、D、G也在同一直线上，设△ABC、△DCE、△GEF的面积分别为S₁、S₂、S₃．当S₁=4，S₂=6时，S₃=         ．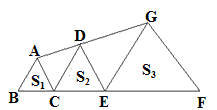

如图1，菱形ABCD的对角线交于点O，AC=2BD，点P是AO上一个动点，过点P 作AC的垂线交菱形的边于M，N两点．设AP＝x，△OMN的面积为y，表示y与x的函数关系大致如图2所示的抛物线．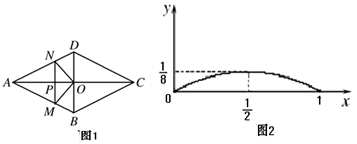

（1）图2所示抛物线的顶点坐标为（    ，    ） ；
（2）菱形ABCD的周长为         ．

如图，在正方形ABCD中，点P是AB上一动点（不与A、B重合），对角线AC，BD相交于点O，过点P分别作AC，BD的垂线，分别交AC，BD于点E，F，交AD，BC于点M，N．下列结论：①△APE≌△AME；
②PM+PN=AC；
③PE²+PF²=PO²；
④△POF∽△BNF；
⑤当△PMN∽△AMP时，点P是AB的中点．
其中正确的结论是           ．

如图，△ABC三个顶点坐标分别为，，，将△ABC绕点B顺时针旋转一定角度后使点A落在轴上，与此同时顶点C恰好落在的图像上， 则k的值为       ．