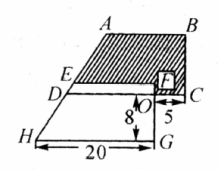
如图,两个相同的直角梯形重叠在一起,将其中一个直角梯形沿 的方向平移,平移的距离为 的长,求阴影部分的面积(单位: ).
如图,已知直线 在 上,且满足 平分 .
(1)求 的度数;
(2)若平行移动 ,那么 的值是否随之发生变化?若变化,找出规律;若不变,求出这个比值;
(3)在平行移动 的过程中,是否存在某种情况,使 ?若存在,求出其度数;若不存在,说明理由.
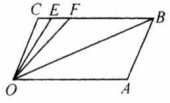
两条直线相交,四个交角中的一个锐角(或一个直角)称为这两条直线的“夹角”(如图),如果在平面上画 条直线,要求它们两两相交,并且“夹角”只能是 其中之一,问:
(1) 的最大值是什么?
(2)当 取最大值时,问所有的“夹角”的和是多少?

在直角坐标系中,有以 为顶点的正方形,设它在折线 上侧部分的面积为 ,求 关于 的函数关系式.
为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:

(1)若甲用户 月份的用气量为 ,则应缴费_____元;
(2)若调价后每月支出的燃气费为 (元),每月的用气量为 ( ), 与 之间的关系如下图所示,求 的值及 与 之间的函数关系式;
(3)在(2)的条件下,若乙用户 月份共用气 ( 月份用气量低于 月份用气量),共缴费 元,乙用户 月份的用气量各是多少?

(1)如图①, 的面积是 ,点 是 的中点,连接 的面积是_____.
(2)如图②,四边形 的面积是 ,点 分别是一组对边 的中点,连接 ,则四边形 的面积是_____.
(3)如图③,点 分别是一组对边 上的点,且 ,若四边形 的面积是 ,连接 ,则四边形 的面积是_____.
(4)如图④, 的面积是 ,点 从点 出发沿 以每秒 个单位长的速度向点 运动,点 从点 出发沿 以每秒 个单位长的速度向点 运动.点 分别从点 同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形 的面积的值是否随着时间 的变化而变化?若不变,请求出这个值;若变化,说明怎样变化的.

如图是甲、乙在一次射击比赛中击中靶的情况(击中靶中心的圆面为 环,靶中各数字表示该数所在圆环被击中所得的环数),每人射击了 次.
(1)请用列表法将他俩射击的成绩统计出来;
(2)请你用学过的统计知识,对他们的 次射击情况进行比较.

阅读下面的材料,再回答问题:
一般地,如果函数 对于自变量取值范围内的任意数 ,都有 ,那么 就叫做奇函数;如果函数 对于自变量取值范围内的任意数 ,都有 ,那么 就叫做偶函数.
例如: .
当 取任意实数时, ,即 ,所以 为奇函数.又如 ,当 取任意实数时, ,即 ,所以 是偶函数.
问题(1):下列函数中:① ;② ;③ ;④ ;⑤ ;所有奇函数是_____,所有偶函数是_____(只填序号)
问题(2):请你再分别写出一个奇函数和一个偶函数.
小华观察钟面(图(1)),了解到钟面上的分针每小时旋转 度,时针每小时旋转 度.他为了进一步研究钟面上分针与时针的旋转规律,从下午 开始对钟面进行了一个小时的观察,为了方便,他将分针与时针原始位置 (图(2))的夹角记为 度,时针与原始位置 的夹角记为 度,(夹角是指不大于平角的角),旋转时间为 ,观察结束后,他利用所得的数据制成图象(图(3)),并求出 与 的函数关系式
请你完成:
(1)求出题图(3)中 与 的函数关系式;
(2)直接写出 两点的坐标,并解释这两点的实际意义;
(3)若小华继续观察一小时,请你在图(3)中补全图象.

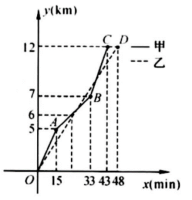
如图,表示甲、乙两名选手在一次自行车越野赛中,路程 随时间 变化的图象(全程).根据图象回答下列问题:
(1)比赛开始多少分钟时,两人第一次相遇?
(2)这次比赛全程是多少千米?
(3)比赛开始多少分钟时,两人第二次相遇?
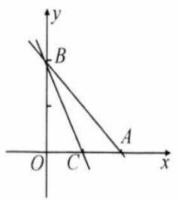
如图,已知直线 与 轴, 轴分别交于点 和点 ,另一直线 经过 ,且把 分成两部分.
(1)若 被分成的两部分面积相等,求 和 的值;
(2)若 被分成的刑部分的面积比为 ,求 和 的值.
阅读下面的材料:
例1:求函数 的反函数;
解:由 ,可得 ,所以原函数 的反函数是 .
例2求函数 的反函数.
解:由 ,可得 ,所以原函数 的反函数是 .
以上两例中,在相应的条件下,一个原函数有反函数时,原函数中自变量 的取值范围就是它的反函数中函数值 的取值范围,原函数中函数值 的取值范围就是它的反函数中自变量 的取值范围,通过以上内容完成下面任务.
(1)求函数 的反函数;
(2)函数 的反函数的函数值的取值范围为_____;
| A. |
|
B. |
|
C. |
|
D. |
|
(3)下列函数中反函数是它本身的是_____(填序号即可).
① ;② ;③ ;④ ;⑤