某班参加一次智力竞赛,共 三题,每题或者得满分或者得零分,其中题 满分 分,题 ,题 满分分别为 分.竞赛结果,每个学生至少答对了一题,三题全答对的有 人,答对其中两道题的有 人,答对题 的人数与答对题 的人数之和为 人,答对题 的人数与答对题 的人数之和为 ,答对题 的人数与答对题 的人数之和为 .问这个班的平均成绩是多少分?
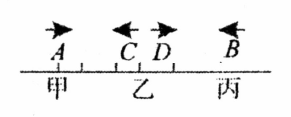
如图,乙地是甲、丙两地的中点, 从甲地, 从丙地, 从乙地分别沿图示的方向同时出发.若 出发后 时遇到 时遇到 时追上 .求 出发后多久遇到 ?多久追上 ?
为何值时,方程组
(1)有唯一一组解;
(2)无解;
(3)有无穷多组解.
如图,能否在图中的四个圆圈内填入 个互不相同的数,使得任意两个圆圈中填的数的平方和等于另外两个圆圈中所填数的平方和?如果能填,请填出一个例子;如果不能填,请说明理由.

某市为鼓励节约用水,对自来水的收费标准作如下规定:每月每户用水不超过 的部分按 元/ 收费;超过 而不超过 的部分按 元 收费;超过 的部分按 元/ 收费.某月甲户比乙户多缴水费 元,乙户比丙户多缴水费3.75元,问甲、乙、丙三户该月各缴水费多少元?(自来水按整数吨收费)
某项工程,如果由甲、乙两队承包, 天完成,需付 元,由乙、丙两队承包, 天完成,需付 元;由甲、丙两队承包, 天完成,需付 元.现在工程由一个队单独承包,在保证一周完成的前提下,哪个队的承包费用最少?
甲、乙两班同时从学校 出发去距离学校 的军营 军训,甲班学生步行速度 ,乙班学生步行速度为 ,学校有一辆汽车,该车空车速度为 ,载人时的速度为 ,且这辆汽车一次恰好只能载一个班的学生,现在要求两个班的学生同时到达军营,问他们至少需要多长时间才能到达?
已知 是满足 的整数,并且使二元一次方程组 有整数解,问这样的整数 有多少个?
已知关于 的二元一次方程 ,当 每取一个值时就有一个方程,而这些方程有一个公共解,你能求出这个公共解,并证明对任何 值它都能使这个方程成立吗?
已知在平面直角坐标系中点 ,点 ,且满足 .
(1)求点 ,点 的坐标;
(2)已知点 ,点 从 点出发,沿 轴负方向以 个单位每秒的速度移动.同时点 从 点出发,沿 轴负方向以 个单位每秒的速度移动,某一时刻,如图②所示,且 .求点 移动的时间?
(3)在(2)的条件下, 交 轴于 ,作 的角平分线交于点 ,如图③所示,判断 是否为定值,若是定值求其值;若不是定值,请说明理由.
