已知在平面直角坐标系中点 ，点 ，且满足 ．
（1）求点 ，点 的坐标;
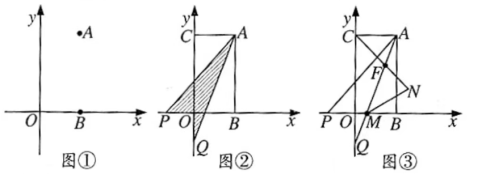
（2）已知点 ，点 从 点出发，沿 轴负方向以 个单位每秒的速度移动．同时点 从 点出发，沿 轴负方向以 个单位每秒的速度移动，某一时刻，如图②所示，且 ．求点 移动的时间?
（3）在（2）的条件下， 交 轴于 ，作 的角平分线交于点 ，如图③所示，判断 是否为定值，若是定值求其值；若不是定值，请说明理由．
相关试题
中，
，且
，
的周长为14 ,将
的位置。
的周长。
下图是按一定规律排列的方程组集合和它解的集合的对应关系图，若方程组集合中的方程组自左至右依次记作方程组1、方程组2、方程组3、……方程组n．
(1)将方程组1的解填入图中； (2)请依据方程组和它的解变化的规律，将方程组n和它的解直接填入集合图中；
(3)若方程组
的解是
，求m、n的值，并判断该方程组是否符合 (2)中的规律？
七(3)班学生参加学校组织的“绿色奥运”知识竞赛，老师将学生的成绩按10分的组距分段，统计每个分数段出现的频数，填入频数分布表，并绘制频数分布直方图．
(1)频数分布表中a=___________，b=_____________；
(2)把频数分布直方图补充完整；
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖，一等奖奖励作业本15本，二等奖奖励作业本10本．已知这部分学生共获得作业本335本，则一等奖和二等奖各多少人？．
如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2，且∠3=115°，求∠ACB的度数．
，
，
．
________________； (2)求
的值．
粤公网安备 44130202000953号