平面上有 条直线,无任何三条交于一点,欲使它们出现 个交点,怎样安排才能办到?(只要求画出符合条件的 条直线)
能否在平面上画出 条直线(任意 条都不共点),使得它们中的每条直线都恰好与另 条直线相交?如果能,请画出一例,如果不能,请简述理由.
编号为 到 的 个弹珠被分别放在两个篮子 和 中, 号弹珠在篮子 中,把这个弹珠从篮子 移至篮子 中,这时篮子 中的弹珠号码数的平均数等于原平均数加 篮中弹珠号码数的平均数也等于原平均数加 ,问原来在篮子 中有多少个弹珠?
我国是水资源比较贫乏的国家之一,各地采用了价格调控等手段来达到节约用水的目的.某市用水收费的方法是:水费 基本费十超额费十定额损耗费.若每月用水量不超过最低限量 时,只付基本费 元和每月的定额损耗费 元;若用水量超过 时,除了付同上的基本费和定额损耗费外,超过部分每立方米付 元的超额费.已知每户每月的定额损耗费不超过 元.
(1)当月用水量为 时,支付费用为 元,写出 关于 的函数关系式;
(2)该市一家庭今年一季度的用水量和支付费用见下表,根据表中数据求 .

如图,在四边形 中, .点 从点 出发,以 的速度向 点运动;点 从点 同时出发,以 的速度向点 运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为 .
(1) 为何值时,四边形 是矩形?
(2) 为何值时,四边形 是平行四边形?
(3)在其它条件不变的情况下,能否通过改变点 的运动速度,使得四边形 是菱形?

某商场计划采购甲、乙、丙三种型号的“格力”牌空调共 台.三种型号的空调进价和售价如下表:

商场计划投入总资金 万元,所购进的甲、丙型号空调数量相同,乙型号数量不超过甲型号数量的一半,若设购买甲型号空调 台,所有型号空调全部售出后获得的总利润为 元.
(1)求 与 之间的函数关系式;
(2)商场如何采购空调才能获得最大利润
(3)由于原材料上涨,商场决定将丙型号空调的售价提高 元( ),其余型号售价不变,则商场又该如何采购才能获得最大利润?
如图,从如图①所示的等边三角形开始,把它各边分成相等的三段,在中间一段上向外画出一个小等边三角形,形成如图②所示的六角星图形;再在六角星各边上用同样的方法向外画出更小的等边三角形,形成如图③所示的有 个尖角的图形,然后,在其各边上再用同样的方法向外画出更小的等边三角形如图④,如此继续下去,图形的轮廓就能形成分支越来越多的曲线,这就是瑞典数学家科赫将雪花理想化得到的科赫雪花曲线.

如果设原等边三角形的边长为 ,不妨把每一次图形的变化过程叫做“生长”,例如第一次生长后得到图②,每个小等边三角形的边长为 ,所形成的图形的周长为 ,请填写下表(用含 的代数式表示).
第一次生长后 |
第二次生长后 |
第三次生长后 |
… |
第 次生长后 |
|
每个小等边三角形的边长 |
|
… |
|||
所形成图形的周长 |
|
… |
有 名待业人员参加某企业甲、乙、丙三个部门招聘,到各部门报名的人数百分比见图表①,该企业各部门的录取率见图表②( )

(1)到乙部门报名的人数有_____人,乙部门的录取人数是_____人,该企业的录取率为_____;
(2)如果到甲部门报名的人员中有一些人员改到丙部门报名,在保持各部门录取率不变的情况下,该企业的录取率将恰好增加 ,问有多少人从甲部门改到丙部门报名?
问题探究:
(1)请你在图①中做一条直线,使它将矩形 分成面积相等的两部分;
(2)如图②,点 是矩形 内一点,请你在图②中过 点作一条直线,使它将矩形 分成面积相等的两部分.
问题解决:
(3)如图③,在平面直角坐标系 中,多边形 的顶点坐标分别是 .若直线 经过点 ,且将多边形 分割成面积相等的两部分,求直线 的函数表达式.

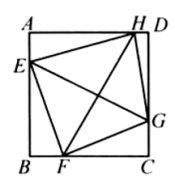
如图,四边形 是正方形 的内接四边形, 与 都是锐角,已知 ,四边形 的面积为 .求正方形 的面积.
如图,四边形 是 的内接四边形。
(1)若 或 ,求证 ;
(2)若 ,问是否能推出 或 ?证明你的结论.
