初中数学解答题

如图1，在△ABC中，AB=AC，点D，E分别在AB和AC上，且∠ADC=∠AEB=90°，则CD=BE．探究发现：如图2，在△ABC中，仍然有条件“AB=AC，点D，E分别在AB和AC上”．若∠ADC＋∠AEB=180°，则CD与BE是否仍相等？若相等，请证明；若不相等，请举反例说明．

已知x+y=4，xy=-12，求（1）x²+y²的值；（2）求（x-y）²的值．

先化简，后求值：已知：[（x-2y）²-2y（2y-x）]÷2，其中x=1，y=2．

若|a|=4，|b|=2，且a＜b，求a－b的值．

两根同样长的蜡烛，点完一根粗蜡烛要2小时，而点完一根细蜡烛要1小时，一天晚上停电，小芳同时点燃了这两根蜡烛看书，若干分钟后来电了，小芳将两支蜡烛同时熄灭，发现粗蜡烛的长是细蜡烛2倍，问：停电﹙  ﹚分钟？

A．30

B．40

C．50

D．60

如图，在ΔABC与ΔDCB 中，AC与BD 交于点E，且，∠A=∠D，AB=DC．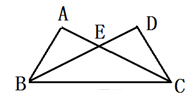

（1）求证：ΔABE≌ΔDCE
（2）当∠AEB=70°时，求∠EBC的度数．

（本题3分）如图，在网格纸上，画出所给图形关于直线l对称的图形．

（本题8分）学校图书馆上周借书记录如下（超过50册的部分记为正，少于50册的部分记为负）：

星期一	星期二	星期三	星期四	星期五
0	+8	+6	-2	-7

（1）上星期五借出图书________册．
（2）上星期二比上星期五多借出图书________册。
（3）上周平均每天借出图书多少册？（一周以5天计算）

在数轴上表示下列各数，并比较它们的大小．
－2，0，1，1．5， ．

已知函数y=
（1）若这个函数是一次函数，求m的值;
（2）若这个函数是二次函数，则m的值应怎样？

已知一元二次方程k+（2k-1）x+k+2=0有两个不相等的实数根，求k的取值范围.

解下列一元二次方程：（每小题4分，共16分）
（1）
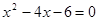
（2）
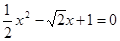
（3）
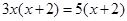
（4）

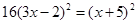
如图，△ABC中，AB=8厘米，AC=16厘米，点P从A出发，以每秒2厘米的速度向B运动，点Q从C同时出发，以每秒3厘米的速度向A运动，其中一个动点到端点时，另一个动点也相应停止运动，那么，当以A、P、Q为顶点的三角形与△ABC相似时，运动时间是多少？

如图，直线OC、BC的函数关系式分别是y₁=x和y₂=﹣2x+6，动点P（x，0）在OB上运动（0＜x＜3），过点P作直线m与x轴垂直．

（1）求点C的坐标，并回答当x取何值时y₁＞y₂？
（2）设△COB中位于直线m左侧部分的面积为s，求出s与x之间函数关系式．
（3）当x为何值时，直线m平分△COB的面积？

如图，在Rt△ABC中，∠C=90°，∠ABC的平分线BD交AC于点D，DE⊥DB交AB于点E，设⊙O是△BDE的外接圆．

（1）求证：AC是⊙O的切线；
（2）若DE=2，BD=4，求AE的长．