下列三个命题:①圆既是轴对称图形又是中心对称图形;②垂直于弦的直径平分弦;③相等的圆心角所对的弧相等.其中真命题的是( )
| A.①② | B.②③ | C.①③ | D.①②③ |
如图,⊙O1、⊙O2内切于点A,其半径分别是6和3,将⊙O2沿直线O1O2平移至两圆外切时,则点O2移动的长度是( )
| A.3; | B.6; |
| C.12; | D.6或12. |
已知⊙O的半径为8,点P到圆心O的距离为3,那么点P与⊙O的位置关系是
| A.点P在⊙O上 | B.点P在⊙O内 |
| C.点P在⊙O外 | D.无法确定 |
如图,点A、B、C都在 上,若∠ACB=46°,则∠AOB的度数是
上,若∠ACB=46°,则∠AOB的度数是
| A.23° | B.46° | C.60° | D.92° |
如图4,两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C,则AB的长为( )
| A.4cm | B.5cm | C.6cm | D.8cm |
如图①,直线AB的解析式为 (
( )与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A.
)与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A.求C点的坐标;
如图②,过
 作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;在⑵的条件下,连接
 与⊙
与⊙ 交于点G,点P为劣弧G F上一个动点,连接GP与EF的延长线交于H点,连接EP与OG交于I点,当P在劣弧G F运动时(不与G、F两点重合),
交于点G,点P为劣弧G F上一个动点,连接GP与EF的延长线交于H点,连接EP与OG交于I点,当P在劣弧G F运动时(不与G、F两点重合), 的值是否发生变化,若不变,求其值,若发
的值是否发生变化,若不变,求其值,若发 生
生 变化,求出其值的变化范围.
变化,求出其值的变化范围.


如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP= ,PQ2=
,PQ2=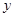 ,则
,则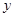 与
与 的函数图象大致是
的函数图象大致是

如图,点A,B,C均在⊙O上,∠ACB=35°,则∠AOB的度数为
| A.20° | B.40° | C.60° | D.70° |
已知:如图8,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.(12)
求证:(1)AD=BD; (2)DF是⊙O的切线.