初中数学圆幂定理试题

将半径为30cm，中心角为120°的扇形铁皮，做成一个圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），则圆锥容器的底面半径为( ▲  )

A．10cm

B．30cm

C．40cm

D．300cm

如右图中，圆与圆之间不同的位置关系有( ▲  )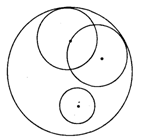
 

A．2种	B．3种
C．4种	D．5种

（本题8分）如图，AB是⊙O的直径，BC是弦，∠ABC的平分线BD
交⊙O于点D，DE⊥BC，交BC的延长线于点E，RD交AC于点F．

(1)求证：DE是⊙O的切线；
(2)若CE＝2，ED＝4，求⊙O的半径．

如图，两圆⊙O₁和⊙O₂相交于A、B两点，DBC和EAO₁都是直线，且∠AO₁C＝140°，那么∠E＝ ▲ ．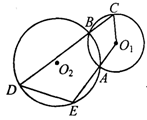

如图，P为⊙O外一点，PA、PB分别切⊙O于A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA＝5，则△PCD的周长为 ▲ ．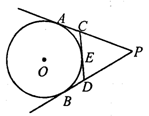

一圆锥的母线长为6cm，它的侧面展开图的圆心角为120°，则这个圆锥的底面半径r为   ▲ cm．

如图，⊙O是△ABC的外接圆，已知∠ABO＝50°，则∠ACB的大小为

A．40°	B．30°
C．45°	D．50°

（本小题满分8分）如图1，正方形ABCD是一个6 × 6网格电子屏的示意图，其中每个小正方形的边长为1．位于AD中点处的光点P按图2的程序移动．

（1）请在图1中画出光点P经过的路径；
（2）求光点P经过的路径总长（结果保留π）．

如图，在5×5正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是

A．点P

B．点Q

C．点R

D．点M

如图，⊙O的直径为10，弦AB的长为8，M是弦AB上的动点，则OM的长的取值范围是____________

有4个命题：
①直径相等的两个圆是等圆；
②长度相等的两条弧是等弧；
③圆中最大的弦是通过圆心的弦；
④在同圆或等圆中,相等的两条弦所对的弧是等弧．其中真命题是__________________

如图，AB是⊙O的直径，它把⊙O分成上、下两个半圆，
自上半圆上一点C作弦CD⊥AB，∠OCD的平分线交⊙O于点P，当C在上半圆（不包括A、B两点）上移动时，点P（ ）

A．到CD的距离保持不变	B．位置不变
C．随C点的移动而移动	D．等分

如图，已知A、B、C、D均在已知圆上，AD‖BC，CA平分∠BCD，
∠ADC＝，四边形ABCD周长为10.

（1）求此圆的半径；
（2）求圆中阴影部分的面积．

(5分)如图,已知⊙O直径为4cm,点M为弧AB的中点,弦MN、AB交于点P,
APM=60°,求弦MN的长.

(5分)