(本小题满分8分)如图1,正方形ABCD是一个6 × 6网格电子屏的示意图,其中每个小正方形的边长为1.位于AD中点处的光点P按图2的程序移动.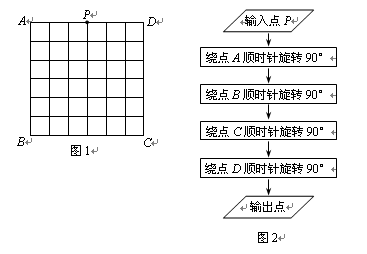
(1)请在图1中画出光点P经过的路径;
(2)求光点P经过的路径总长(结果保留π).
相关知识点
推荐套卷
(本小题满分8分)如图1,正方形ABCD是一个6 × 6网格电子屏的示意图,其中每个小正方形的边长为1.位于AD中点处的光点P按图2的程序移动.
(1)请在图1中画出光点P经过的路径;
(2)求光点P经过的路径总长(结果保留π).