初中数学圆幂定理试题

(本小题满分1 0分)
已知：如图，以矩形ABCD的对角线AC的中点O为圆心，OA长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥ A C，垂足为K。过D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H．

(1)求证：AE=CK；
(2)如果AB=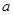，AD=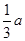 (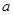为大于零的常数)，求BK的长：
(3)若F是EG的中点，且DE=6，求⊙O的半径和GH的长．

(本小题满分8分)
某学校要在围墙旁建一个长方形的中药材种植实习苗圃，苗圃的一边靠围墙(墙的长度不限)，另三边用木栏围成，建成的苗圃为如图所示的长方形ABCD。已知木栏总长为120米，设AB边的长为x米，长方形ABCD的面积为S平方米．

(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围)．当x为何值时，S取得最值(请指出是最大值还是最小值)?并求出这个最值；
(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆，其圆心分别为和，且到AB、BC、AD的距离与到CD、BC、AD的距离都相等，并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面，以方便同学们参观学习．当(l)中S取得最值时，请问这个设计是否可行?若可行，求出圆的半径；若不可行，清说明理由．

已知⊙O的面积为9π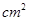，若点0到直线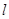的距离为π，则直线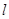与⊙O的位置关系是

A．相交

B．相切

C．相离

D．无法确定

如图，AB是⊙O的直径，点C是BA延长线上一点，CA=1，CD切⊙O于D点，弦DE∥CB，Q是AB上一动点，当DQ⊥AB时Q恰好为OA中点.

(1)求⊙O的半径R．
(2) 当点 Q从点A向点B运动的过程中，图中阴影部分的面积是否发生变化，若发生变化，请你说明理由；若不发生变化，请你求出阴影部分的面积．

已知：如图直线PA交⊙O于A，E两点，过A点作⊙O的直径AB.PA的垂线DC交⊙O于点C，连接AC，且AC平分∠DAB.
(1) 试判断DC与⊙O的位置关系？并说明理由.
(2) 若DC＝4，DA＝2，求⊙O的直径.

如图，在正方形网格图中建立一直角 坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作：
 
(1) 利用网格确定该圆弧所在圆的圆心D点的 位置（保留画图痕迹），则D点坐标为  ▲   ；
(2) 连接AD、CD，则⊙D的半径为  ▲   (结果保留根号)，∠ADC的度数为  ▲   度；
(3)若扇形DAC是一个圆锥的侧面展开图，求该圆锥底面的半径．(结果保留根号)

如右图，一块含有30º角的直角三角形ABC，在水平桌面上绕点C按顺时针方向旋转到△A’B’C的位置.若BC的长为18cm，那么顶点A从开始到结束所经过的路径长为       ▲    cm．

已知关于ｘ的一元二次方程ｘ²－2(Ｒ＋ｒ)ｘ＋ｄ²＝０有两个相等的实数根，其中Ｒ、ｒ分别为⊙Ｏ₁、⊙Ｏ₂的半径，ｄ为两圆的圆心距，则⊙Ｏ₁与⊙Ｏ₂的位置关系是   ▲   ．

已知Rt△ABC中，∠C＝90º，AC＝5cm，BC＝12cm，则△ABC的内切圆半径为    ▲    cm．

如图，⊙O的直径CD过弦EF的中点G，∠EOD=50°,则∠DCF=   ▲   ．

如图，AB为⊙O的直径，点C在⊙O上，过点C作⊙O的切线交AB的延长线于点D，已知∠D＝30°．

(1)求∠A的度数；
(2)若点F在⊙O上，CF⊥AB，垂足为E，CF＝8，
　　求图中阴影部分的面积（结果保留π及根号）．

已知⊙O的半径OA为1．弦AB的长为，若在⊙O上找一点C，使AC＝，则∠BAC＝ ▲ °．

如图，在⊙O中，∠AOC＝100°， 则∠ABC＝ ▲ °．

如图，以AB为直径的⊙O与AD、DC、BC均相切，若AB＝BC＝4，则OD的长度为

A．             B．           C．          D．2

已知圆锥的母线长是8cm，底面半径为3cm，则圆锥侧面积是

A．12 πcm^2

B．24πcm^2

C．36πcm^2

D．48πcm^2