如图,AB是⊙O的直径,点C是BA延长线上一点,CA=1,CD切⊙O于D点,弦DE∥CB,Q是AB上一动点,当DQ⊥AB时Q恰好为OA中点.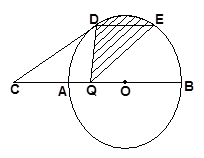
(1)求⊙O的半径R.
(2) 当点 Q从点A向点B运动的过程中,图中阴影部分的面积是否发生变化,若发生变化,请你说明理由;若不发生变化,请你求出阴影部分的面积.
相关知识点
推荐套卷
如图,AB是⊙O的直径,点C是BA延长线上一点,CA=1,CD切⊙O于D点,弦DE∥CB,Q是AB上一动点,当DQ⊥AB时Q恰好为OA中点.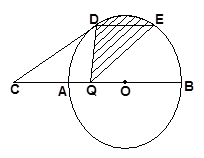
(1)求⊙O的半径R.
(2) 当点 Q从点A向点B运动的过程中,图中阴影部分的面积是否发生变化,若发生变化,请你说明理由;若不发生变化,请你求出阴影部分的面积.