初中数学圆幂定理试题

已知：如图，⊙O的内接△ABC中，∠BAC＝45°，∠ABC＝15°，AD∥OC并交BC的延长线于D，OC交AB于E．

求∠D的度数；
求证：AC²＝AD·CE；
求的值．

已知：如图，∠MAN＝45°，B为AM上的一个定点．若点P在射线AN上，以P为圆心，PA为半径的圆与射AN的另一个交点为C．请确定⊙P的位置，使BC恰与⊙P相切．

画出⊙P；(不要求尺规作图，不要求写画法)
连结BC、BP并填空：
①∠ABC＝______°；
②比较大小：∠ABP______∠CBP．(用“＞”、“＜”或“＝”连接)

已知：如图，AB是⊙O的直径，BC是弦，∠B＝30°，延长BA到D，
使∠ADC＝30°．

求证：DC是⊙O的切线；
若AB＝2，求DC的长．

如图，∠ABC＝90°，O为射线BC上一点，以点O为圆心，长为半径作⊙O，将射线BA绕点B按顺时针方向旋转至BA＇，若BA＇与⊙O相切，则旋转的角度??(0°＜??＜180°)等于______．

如图，⊙O的直径是AB，CD是⊙O的弦，基∠D＝70°，则∠ABC等于______．

如图，PA、PB与⊙O相切，切点分别为A、B，PA＝3，∠P＝60°，若AC为⊙O的直径，则图中阴影部分的面积为(    )

A．       B．
C．        D．

如图，⊙O的半径OA等于5，半径OC与弦AB垂直，垂足为D，若OD＝3，则弦AB的长为(    )

A．10

B．8

C．6

D．4

如图，在平面直角坐标系中，O为坐标原点，P是反比例函数y＝（x＞0）图象上的任意一点，以P为圆心，PO为半径的圆与x、y轴分别交于点A、B．

（1）判断P是否在线段AB上，并说明理由；
（2）求△AOB的面积．

已知⊙O₁与⊙O₂的半径、分别是方程 的两实根，若⊙O₁与⊙O₂的圆心距=5．则⊙O₁与⊙O₂的位置关系是          .

已知扇形的圆心角为120°，半径为9cm，则扇形的面积为　　　　.

如图，AB为⊙O的直径，∠ DCB＝30°, ∠ DAC＝70°,则∠D的度数为

A．70°

B．50°

C．40°

D．30°

如图，BD是直径，过⊙O上一点A作⊙O切线交DB延长线于P，过B点作BC∥PA交⊙O于C，连接AB、AC ，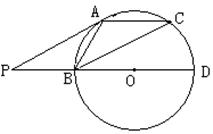

（1）求证：AB = AC
（2）若PA=" 10" ，PB =" 5" ，求⊙O半径．

如图，AB为⊙O直径，BC切⊙O于B，CO交⊙O于D，AD的延长线交BC于E，若∠C = 25°，求∠A的度数．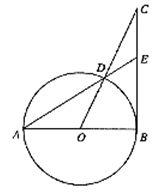

如图，⊙O中，∠ACB＝∠D＝60°，AC＝3，△ABC周长为______.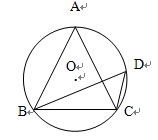

半径分别为6cm和4cm的两圆内切，则它们的圆心距为       cm.