阅读材料：如图23—1，
的周长为
，面积为S,内切圆
的半径为
，探究
与S、之间的关系．连结
，
，
又
，
，
∴
∴
解决问题
：
（1）利用探究的结论，计算边长分别为5，12，13的三角形内切圆半径；
（2）若四边形
存在内切圆（与各边都相切的圆），如图23—2且面积为
，各边长分别为
，
，
，
，试推导四边形的内切圆半径公式；
（3）若一个
边形（为不小于3的整数）存在内切圆，且面积为，各边长分别为
，
，
，
，
，合理猜想其内切圆半径公式（不需说明理由）．
已知：AB是⊙O的弦，OD⊥AB于M交⊙O于点D，CB⊥AB交AD的延长线于C．
（1）求证：AD＝DC；
（2）过D作⊙O的切线交BC于E，若DE＝2，CE=1，求⊙O的半径．
如图，AB是⊙O的直径，BC是弦，∠ABC的平分线BD交⊙O于点D，DE⊥BC，交BC的延长线于点E，BD交AC于点F．⑴求证：DE是⊙O的切线；（2） 若CE=1，ED=2，求⊙O的半径．
在平面直角坐标系
中，矩形ABCO的面
积为15，边OA比OC大2，E为BC的中点，以OE为直径的⊙O′交x轴于D点，过点D作DF⊥AE于F. 
（1） 求OA，OC的长；
（2） 求证：DF为⊙O′的切线；
（3）由已知可得，△AOE是等腰三角形.那么在直线BC上是否存在除点E以外的点P，使△AOP也是等腰三角形？如果存在，请你证明点P与⊙O′的位置关系，如果不存在，请说明理由.
如图所示，AB是⊙O的直径，OD⊥弦BC于点F，且交⊙O于点E，若∠AEC=∠ODB．
（1）判断直线BD和⊙O的位
置关系，并给出证明；
（2）当AB=10，BC=8时，求BD的长．
如图，AB是⊙O的直径，弦BC＝2cm，∠ABC＝60º．
（1）求⊙O的直径；
（2）若D是AB延长线上一点，连结CD，当BD长为多少时，CD与⊙O相切；
（3）若动点E以2cm/s的速度从A
点出发沿着AB方向运动，同时动点F以1cm/s的速度从B点出发沿BC方向运动
，设运动时间为
，连结EF，当
为何值时，△BEF为直角三角形．
如图，AB为⊙O的直径，弦CD⊥AB，垂足为点M，AE切⊙O于点A，交BC的延长线于点E，连接AC.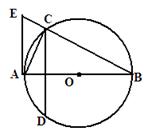
(1)若B=30°，AB=2，求CD的长；
(2)求证：AE2=EB·EC.
如图8，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且AB＝AD＝AO．
（1）求证：BD是⊙O的切线．
（2）若点E是劣弧BC上一点，AE与BC相交于点F，且△BEF的面积为8，cos∠BFA＝
，求△ACF的面积．
如图所示，△ABC内接于⊙O，AD是△ABC的边BC上的高，AE是⊙O的直径，连接BE. 求证：△ABE∽△ADC .
如图，AB是半圆的直径，O为圆心，AD、BD是半圆的弦，且∠PDA=∠PBD。
(1) 判断直线PD是否为⊙O的切线，并说明理由；
(2) 如果ÐBDE=60°，PD=
，求PA的长。
已知，如图，M是弧AB的中点，过点M的弦MN交于点C，设圆O的半径为4厘米，MN=4cm,
(1)求圆心O到弦MN的距离；
(2)求∠ACM的度数。
如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC，AD，BD的长．
粤公网安备 44130202000953号