在平面直角坐标系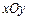 中,矩形ABCO的面
中,矩形ABCO的面 积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于F.
积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于F. 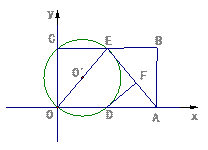
(1) 求OA,OC的长;
(2) 求证:DF为⊙O′的切线;
(3)由已知可得,△AOE是等腰三角形.那么在直线BC上是否存在除点E以外的点P,使△AOP也是等腰三角形?如果存在,请你证明点P与⊙O′的位置关系,如果不存在,请说明理由.
相关知识点
推荐套卷
在平面直角坐标系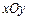 中,矩形ABCO的面
中,矩形ABCO的面 积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于F.
积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于F. 
(1) 求OA,OC的长;
(2) 求证:DF为⊙O′的切线;
(3)由已知可得,△AOE是等腰三角形.那么在直线BC上是否存在除点E以外的点P,使△AOP也是等腰三角形?如果存在,请你证明点P与⊙O′的位置关系,如果不存在,请说明理由.