如图，△ABC中，∠ACB=90°，D是边AB上的一点，且∠A=2∠DCB.E是BC上的一点，以EC为直径的⊙O经过点D。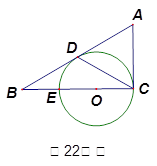
求证:AB是⊙O的切线；
若CD的弦心距为1,BE=ED.求BD的长.
，求
的值．
（2）
．
（2）
相关知识点
推荐套卷
如图，△ABC中，∠ACB=90°，D是边AB上的一点，且∠A=2∠DCB.E是BC上的一点，以EC为直径的⊙O经过点D。求证:AB是⊙O的切线；
若CD的弦心距为1,BE=ED.求BD的长.
粤公网安备 44130202000953号