一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同，其中黄球的个数是白球个数的2倍少5个，已知从袋中摸出一个球是红球的概率是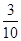
.求袋中红球的个数；
求从袋中摸出一个球是白球的概率；
取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
相关试题
，并把它的解集在数轴上表示出来．（本题5分）
，并写出不等式组的整数解．（本题5分）
； 
；
．
相关知识点
推荐套卷
一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同，其中黄球的个数是白球个数的2倍少5个，已知从袋中摸出一个球是红球的概率是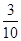.求袋中红球的个数；
求从袋中摸出一个球是白球的概率；
取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
粤公网安备 44130202000953号