如图,在
中,
,
,
,点
从点
以每秒1个单位长度的速度向点
运动(点
不与
重合),过点
作DE∥BC交
于点
.以
为直径作 ⊙O,并在
内作内接矩形
,设点
的运动时间为
秒.
⊙O,并在
内作内接矩形
,设点
的运动时间为
秒.

(1)用含
的代数式表示
的面积
;
(2)当
为何值时,
与直线
相切?
如图7.在⊙O中.弦BC垂直于半径OA.垂足为E.D是优弧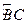 上一点.连接BD.AD.OC,∠ADB=30°.
上一点.连接BD.AD.OC,∠ADB=30°.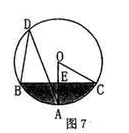
(1)求∠AOC的度教;
(2)若弦BC=6cm.求图中阴影部分的面积.
在圆内接四边形ABCD中,CD为∠BCA外角的平分线,F为弧AD上一点,BC=AF,延长DF与BA的延长线交于E.
⑴求证△ABD为等腰三角形.
⑵求证AC•AF=DF•FE
如图,已知点C在⊙O上,延长直径AB到点P,连接PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)若AC=PC,且PB=3,M是⊙O下半圆弧的中点,求MA的长.
如图,在Rt△ABC中,∠C=90°.BE平分∠ABC交AC于点E,点D在AB上,DE⊥BE于点E.
(1)判断直线AC与△DBE外接圆的位置关系,并证明你的结论;
(2) 若AD=6,AE=6,求BC的长.
若AD=6,AE=6,求BC的长.
如图,AB 为⊙O的直径,AB=4,点C在⊙O上, CF⊥OC,且CF=BF.
为⊙O的直径,AB=4,点C在⊙O上, CF⊥OC,且CF=BF.
(1)证明BF是⊙O的切线;
(2)设AC与BF的延长线交于点M,若MC=6,求∠MCF的大小.
如图,AB 为⊙O的直径,AB=4,点C在⊙O上, CF⊥OC,且CF=BF.
为⊙O的直径,AB=4,点C在⊙O上, CF⊥OC,且CF=BF.
(1)证明BF是⊙O的切线;
(2)设AC与BF的延长线交于点M,若MC=6,求∠MCF的大小.
(本小题满分5分)
已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于点D、E,联结EB交OD于点F.
(1)求证:OD⊥BE;
(2)若DE= ,AB=5,求AE的长.
,AB=5,求AE的长.
如图,有一圆锥形粮堆,其主视图是连长为6m的正三角形ABC,母线AC 的中点处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,求小猫经过的最短路程。(结果保留根号)
的中点处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,求小猫经过的最短路程。(结果保留根号)
如图,AB是⊙O的直径,BC是弦,∠ABC的平分线BD交⊙O于点D,DE⊥BC,交BC的延长线于点E,BD交AC于点F.⑴求证:DE是⊙O的切线;(2) 若CE=1,ED=2,求⊙O的半径.
如图所示,AB是⊙O的直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
(1)判断直线BD和⊙O的位 置关系,并给出证明;
置关系,并给出证明;
(2)当AB=10,BC=8时,求BD的长.
如图8,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
(1)求证:BD是⊙O的切线.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为8,cos∠BFA= ,求△ACF的面积.
,求△ACF的面积.
如图所示,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,连接BE. 求证:△ABE∽△ADC .
如图10,以点M(-1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y=- x- 与⊙M相切于点H,交x轴于点E,交y轴于点F.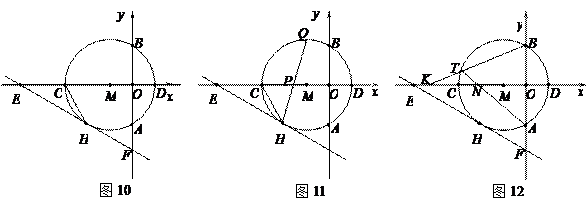
(1)请直接写出OE、⊙M的半径r、CH的长;
(2)如图11,弦HQ交x轴于点P,且DP:PH=3:2,求cos∠QHC的值;
(3)如图12,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a,始终满足MN·MK=a,如果存在,请求出a的值;如果不存在,请说明理由.